Guía UNAM 2024 área 4: Matemáticas reactivos 52 al 62

¡Ya casi terminamos, aspirante! Continuamos con la solución de los reactivos de matemáticas, desde el 52 al 62, de la guía de la UNAM 2024 para las carreras del área 4 de las Humanidades y de las Artes.

¡Resuélvelos por tu cuenta sin mirar la respuesta correcta!

Guía de matemáticas UNAM Área 3

Finalizamos con los 11 reactivos de matemáticas de la guía UNAM, área 4 de las Humanidades y de las Artes.

Reactivo 52

¿Cuál de las siguientes expresiones se obtiene de la Ley de los Senos?

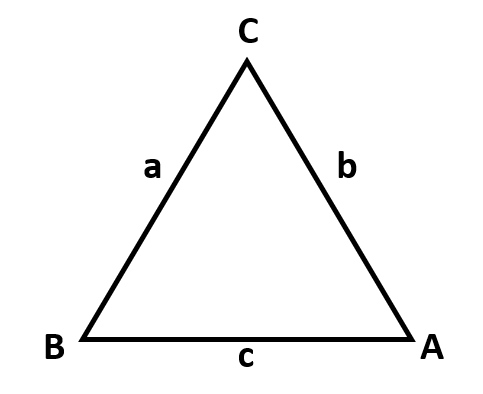
1. $\frac{\mathrm{sen}A}{a}=\frac{\mathrm{sen}B}{b}$
2. $\frac{\mathrm{sen}A}{b}=\frac{\mathrm{sen}B}{a}$
3. $\frac{\mathrm{sen}A}{c}=\frac{\mathrm{sen}B}{a}$
4. $\frac{\mathrm{sen}B}{c}=\frac{\mathrm{sen}A}{b}$

Reactivo 53

El dominio D y el rango R de la función $f\left(x\right)=\frac{{e}^{x}}{-5}$ son

1. $D=\left(-\mathrm{\infty },0\right);R=\left(-\mathrm{\infty },\mathrm{\infty }\right)$
2. $D=\left(0,\mathrm{\infty }\right);R=\left(-\mathrm{\infty },\mathrm{\infty }\right)$
3. $D=\left(-\mathrm{\infty },\mathrm{\infty }\right);R=\left(0,\mathrm{\infty }\right)$
4. $D=\left(-\mathrm{\infty },\mathrm{\infty }\right);R=\left(-\mathrm{\infty },0\right)$

Reactivo 54

¿Cuál es la ecuación de la asíntota vertical de la función $f\left(x\right)=2\mathrm{log}\left(x-3\right)$?

1. $x=3$
2. $y=-3$
3. $x=-3$
4. $y=3$

Reactivo 55

¿Cuál es la distancia entre los puntos $A\left(-7, -2\right)$ y $B\left(2, 7\right)$?

1. 162
2. $\sqrt{50}$
3. $\sqrt{162}$
4. 50

Reactivo 56

¿Cuál es la pendiente de la recta que pasa por los puntos $A(3, 2)$ y $B(1, 5)$?

1. 3
2. $\frac{3}{2}$
3. 1
4. $-\frac{3}{2}$

Reactivo 57

¿Cuál de las siguientes ecuaciones corresponde a una circunferencia con centro en el origen y radio 2?

1. ${x}^{2}+{y}^{2}-4=0$
2. ${x}^{2}+{y}^{2}-2=0$
3. ${x}^{2}-{y}^{2}-2=0$
4. ${x}^{2}-{y}^{2}-4=0$

Reactivo 58

Determina el centro y el radio de la circunferencia a partir de su ecuación.

${\left(x+4\right)}^{2}+{\left(y-6\right)}^{2}=49$

1. $C(-4, 6); r=7$
2. $C(4, –6); r=7$
3. $C\left(–4, 6\right); r=49$
4. $C(4, –6); r=49$

Reactivo 59

Calcula el vértice de la parábola ${\left(y-3\right)}^{2}=12x-24$.

1. $V=\left(\mathrm{2,3}\right)$
2. $V=\left(\mathrm{3,2}\right)$
3. $V=\left(-3,-2\right)$
4. $V=\left(-2,-3\right)$

Reactivo 60

Determina las coordenadas de los focos de una elipse cuya ecuación es $9{x}^{2}+{y}^{2}=9$.

1. ${F}_{1}=\left(-\sqrt{8},0\right);{F}_{2}=\left(\sqrt{8},0\right)$
2. ${F}_{1}=\left(-\sqrt{10},0\right);{F}_{2}=\left(\sqrt{10},0\right)$
3. ${F}_{1}=\left(0,-\sqrt{8} \right);{F}_{2}=\left(0, \sqrt{8}\right)$
4. ${F}_{1}=\left(0,-\sqrt{10} \right);{F}_{2}=\left(0, \sqrt{10}\right)$

Reactivo 61

Lugar geométrico en el plano cartesiano en el que el valor absoluto de la diferencia de sus distancias a dos puntos fijos en el mismo plano resulta siempre igual a una constante, positiva y menor que la distancia entre dichos puntos fijos.

1. Circunferencia
2. Parábola
3. Elipse
4. Hipérbola

Reactivo 62

Al trasladar la circunferencia ${x}^{2}+{y}^{2}-36=0$ al centro $C\left(-\mathrm{2,4}\right)$, ¿cuál sería su ecuación?

1. ${\left(x-4\right)}^{2}+{\left(y+16\right)}^{2}=36$
2. ${\left(x+4\right)}^{2}+{\left(y-16\right)}^{2}=36$
3. ${\left(x+2\right)}^{2}+{\left(y-4\right)}^{2}=36$
4. ${\left(x-2\right)}^{2}+{\left(y+4\right)}^{2}=36$

Respuestas correctas:

• 52. a
• 53. d
• 54. a
• 55. c
• 56. d
• 57. a
• 58. a
• 59. a
• 60. c
• 61. d
• 62. c