¡Hola aspirante! En este post vamos a resolver los reactivos de la guía de Física para la UAM en la división de Ciencias Biológicas y de la Salud (CBS); desde el problema 86 al 94.

Desarróllalos por tu cuenta y luego regresa para comprobar resultados o aclarar dudas. La única vía para entender física, es practicar y estudiar la teoría.
A continuación, un resumen de la convocatoria UAM para el 2022.
- Número de convocatorias: Dos al año.
- Fechas de registro: marzo y agosto del 2022
- Oferta académica: 82 carreras
- Divisiones académicas: 6
- Modalidad: en línea
Estructura del examen de ingreso UAM 2022
El examen de ingreso a la UAM se divide en dos partes:
- La prueba de aptitud
- La prueba de conocimientos específicos
La prueba de aptitud consta, a su vez, de dos partes: una de razonamiento matemático y otra de razonamiento verbal. Como dato extra, esta sección del examen se mantiene en todas las divisiones.
La segunda parte corresponde a los conocimientos específicos de la división a la que pertenece tu carrera. En el caso de Ciencias Biológicas y de la Salud (CBS), las asignaturas son: química, física y biología.
El siguiente, es un resumen de los subtemas en cada una de las asignaturas ya mencionadas.
Física
- Estándares de medición
- Cinemática
- Dinámica
- Termodinámica
- Electromagnetismo
- Óptica
Química
- Química general
- Química inorgánica
- Química orgánica
Biología
- Evolución
- Bioquímica
- Citología
- Genética
- Histología
- Anatomía y fisiología
- Diversidad de organismos
- Ecología
- Educación para la salud
Resumen de reactivos en cada parte del examen.
| Área | Reactivos | Porcentaje |
|---|---|---|
| Razonamiento verbal | 20 | 25% |
| Razonamiento matemático | 20 | 25% |
| Conocimientos específicos | 40 | 50% |
| Total | 80 | 100% |
Temario de Física para CBS
Este es el temario específico en materia de física para la prueba de ingreso a la UAM. Aunque parece extenso, la cantidad de reactivos en la guía es escasa. Te recomiendo continuar realizando ejercicios.
Estándares de medición
- Análisis dimensional.
- Sistema internacional de unidades.
- Magnitudes físicas, escalares y vectoriales, fundamentales y derivadas.
- Notación científica.
- Conversión de unidades.
Cinemática
- Conceptos de desplazamiento, velocidad y aceleración.
- Movimiento rectilíneo uniforme y acelerado.
- Movimiento circular y tiro parabólico.
Dinámica
- Conceptos de inercia, momento, energía cinética, energía potencial, trabajo y potencia.
- Leyes de Newton.
Termodinámica
- Leyes de la termodinámica.
- Leyes de los gases.
Electromagnetismo
- Carga eléctrica.
- Ley de Coulomb.
- Potencial eléctrico.
- Resistencia y ley de Ohm.
Óptica
- Óptica física. Frecuencia, amplitud, onda.
- Óptica geométrica. Absorción y difusión de la luz.
- Espectro de la luz solar.
Guía UAM CBS de Física resuelta
Finalizada la introducción, vamos con la solución paso a paso de los reactivos de física para la división de Ciencias Biológicas y de la Salud en la Universidad Autónoma Metropolitana.
Reactivo 86: Velocidad media
Un automóvil recorre una distancia de 450 km durante un periodo de 10 h ¿Cuál es la velocidad media?
- 450\frac{km}{h}
- 45\frac{km}{h}
- 4.5\frac{km}{h}
- 4500\frac{km}{h}
- 0.45\frac{km}{h}
Solución:
La velocidad promedio permite cuantificar la distancia que ha recorrido un cuerpo durante un intervalo de tiempo determinado y se calcula como:
{v}_{m}=\frac{\Delta x}{\Delta t}=\frac{{x}_{2}-{x}_{1}}{{t}_{2}-{t}_{1}}
En nuestro caso, el problema indica la distancia que ha recorrido el automóvil \Delta x=450 km y también el intervalo de tiempo en el que lo ha hecho \Delta t=10 h . Sustituimos en la ecuación y calculamos.
{v}_{m}=\frac{\Delta x}{\Delta t}=\frac{450 km}{10 h}=45\frac{km}{h}
La velocidad media del automóvil fue de 45\frac{km}{h} .
Comparando con las opciones, seleccionamos como respuesta correcta a la B.
Reactivo 87: Inercia
Una medida de la inercia de un cuerpo es su:
- Forma
- Tamaño
- Rigidez
- Masa
- Temperatura
Solución:
La inercia, es la cualidad física que posee un cuerpo de mantenerse en estado de reposo o en movimiento uniforme (sin aceleración) relativo. Puede pensarse en la inercia como la resistencia que opone un cuerpo a cambiar su estado de reposo, la intensidad o dirección de su movimiento rectilíneo.
La interpretación más clara de la inercia es pensar que los cuerpos no pueden por sí mismos cambiar su estado de movimiento. Necesitan de una fuerza externa, de una interacción para dejar el estado de inmovilidad relativa que poseen.
En base al análisis anterior, seleccionamos como medida de la inercia de un cuerpo a su Masa. La respuesta correcta es la D.
Reactivo 88: Disparo de proyectiles
Al ser disparada una bala de cañón, su aceleración al estar en el aire es:
- Cero
- Hacia arriba primero y hacia abajo después
- Hacia abajo primero y hacia arriba después
- Hacia arriba todo el tiempo
- Constante y hacia abajo
Solución:
Sin considerar la resistencia al viento de los objetos, cuando un proyectil es lanzado (disparado) con un ángulo de inclinación \theta a una velocidad inicial {v}_{o} inmediatamente la fuerza gravitatoria comienza a actuar sobre él.
En dirección vertical y hacia abajo, la aceleración gravitatoria curva la trayectoria del proyectil provocando que sea igual una parábola invertida.
Ecuaciones del movimiento de proyectiles.
{v}_{x}=\left|{v}_{o}\right|cos \theta
{v}_{y}=\left|{v}_{o}\right|sin \theta -gt
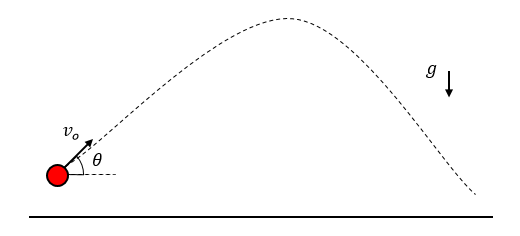
Concluimos seleccionando la opción E como la respuesta correcta.
Reactivo 89: Trabajo eléctrico
El trabajo que se hace al mover una carga contra un campo eléctrico es:
- W=Vq
- V=Ed
- P=VI
- I=\frac{V}{R}
- R=IE
Solución:
Por definición, el trabajo se define como el desplazamiento que provoca una fuerza al interactuar con un cuerpo. La forma de medirlo, de forma general es mediante la siguiente ecuación integral:
W={\int }_{a}^{b}\overrightarrow{F}\bullet d\overrightarrow{l}
Donde \overrightarrow{F} es la fuerza que actúa sobre el cuerpo y d\overrightarrow{l} es un diferencial de longitud en dirección al movimiento.
¿Cómo trasladamos este concepto a cargas eléctricas? Recordemos que cuando una carga eléctrica se encuentra inmersa en un campo eléctrico, experimenta una fuerza que puede expresarse como:
{\overrightarrow{F}}_{e}=q\overrightarrow{E}
Sustituyendo en la ecuación de trabajo.
W={\int }_{a}^{b}q\overrightarrow{E}\bullet d\overrightarrow{l}
La carga puede salir como una constante, quedando la integral de lineal del campo eléctrico.
W=q{\int }_{a}^{b}\overrightarrow{E}\bullet d\overrightarrow{l}
Ahora, supongamos que la trayectoria es rectilínea y que el campo eléctrico es constante en el entorno de la carga. La integral queda como:
W=q{\int }_{a}^{b}Edlcos 0 =q{\int }_{a}^{b}Edl=qE\left(b-a\right)
Además, como la fuerza eléctrica es conservativa y también lo es el campo que la genera, podemos decir que el trabajo eléctrico es igual a menor la variación de energía potencial.
W=-\Delta U=qE\left(b-a\right)
Pasamos al otro lado la carga y nos queda que:
-\frac{\Delta U}{q}=E\left(b-a\right)\to -\frac{\Delta U}{q}=Ed
Al producto del campo eléctrico por la distancia le llamaremos diferencia de potencial.
Ed=-\Delta V
Sustituyendo en la ecuación nos queda:
W=q\Delta V
Para simplificar la notación, sólo se indica como V .
W=qV
El trabajo eléctrico es igual al producto de la carga en movimiento por la diferencia de potencial a la que es sometida dicha carga.
Seleccionamos como respuesta correcta a la opción A.
Reactivo 90: Reflexión de la luz
Un espejo plano refleja los rayos de luz en los que no pasa:
- Una imagen de luz
- Una aberración esférica
- Un haz de rayos de luz en el mismo orden en que llegan
- Una inversión de derecha a izquierda
- Una sombra continua
Solución:
Los espejos planos tienen la particularidad de reflejar la luz que llega a ellos con el mismo ángulo de incidencia si se mide respecto a la normal. Esto provoca que la imagen reconstruida (luego de la reflexión) parezca venir de un punto virtual detrás del espejo y paralelo al objeto real.
Por ello, un rayo de luz que incide paralelo a la normal del espejo plano se refleja también paralelo a la normal. En términos de las opciones que se encuentran en los incisos, corresponde con un haz de rayos de luz en el mismo orden en que llegan.
Seleccionamos como opción correcta a la del inciso C.
Reactivo 91: Lentes
Una lente convergente es:
- Delgada en centro y gruesa en los bordes
- Del mismo grosor
- Solo gruesa en el centro
- Solo delgada en el centro
- Gruesa en el centro y delgada en el borde
Solución:
Una lente es convergente si los rayos de luz refractados se cruzan, todos en un mismo punto. Estructuralmente, una lente convergente es más gruesa en el centro y delgada en los bordes.
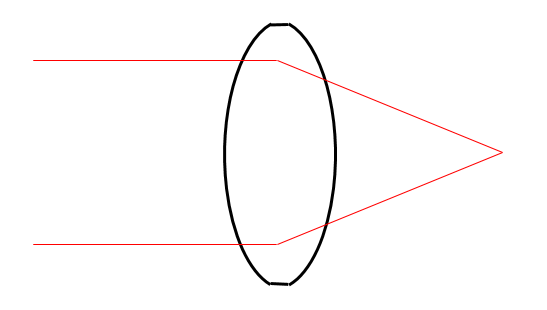
Comparando con las opciones, la respuesta correcta es la E.
Reactivo 92: Sistemas termodinámicos
Cuando en un proceso termodinámico no entra ni sale calor, es de tipo:
- Isotérmico
- Isobárico
- Adiabático
- Isomórfico
- Isoestérico
Solución:
El calor y el trabajo son los únicos mecanismos a través de los cuales, un sistema puede transferir energía o recibir energía de su entorno. Todo sistema termodinámico del que no entra ni sale calor, se considera adiabático. Es decir Q=0 . En base a los términos de cada inciso, seleccionamos como respuesta correcta a la opción C.
Reactivo 93: Cero absoluto
El límite _______ para la temperatura de un cuerpo, recibe el nombre de cero absoluto y corresponde a una situación de energía ________ de los átomos y moléculas de una sustancia.
- Inferior, cinética máxima
- Inferior, mecánica mínima
- Superior, cinética máxima
- Superior, cinética mínima
- Inferior, cinética mínima
Solución:
El denominado cero absoluto, es un punto en el cual las moléculas de una sustancia se encuentran en el nivel más bajo posible.
Desde el punto de vista clásico, la temperatura está asociada con la energía y el movimiento de las moléculas en una sustancia; en el cero absoluto dichas moléculas carecen de movimiento, de allí la afirmación sobre la “mínima energía cinética”.
En base a nuestro análisis, la combinación correcta de palabras es la del inciso E Inferior, cinética mínima.
El límite inferior para la temperatura de un cuerpo, recibe el nombre de cero absoluto y corresponde a una situación de energía cinética mínima de los átomos y moléculas de una sustancia.
Reactivo 94: Gas ideal
La ecuación que representa a un gas ideal es:
- c=\frac{AQ}{AT}
- g=\frac{GMe}{R{e}^{2}}
- PV=nRT
- Q=\left(vq-vi\right)+w
- W=\int pdv
Solución:
Se denomina Gas Ideal a aquella sustancia gaseosa que satisface la siguiente ecuación de estado:
PV=nRT
Donde:
- P es la presión del gas en kPa
- V es el volumen que ocupa el gas en {m}^{3}
- R es la constante universal de los gases
- n numero de moles de la sustancia
- T temperatura del gas
Comparando con las opciones del problema, queda claro que la respuesta es la opción C.

