Guía IPN 2024 Cálculo Diferencial: 40 Ejercicios Resueltos

Te ayudamos a alcanzar el objetivo de ser un aspirante seleccionado en el Instituto Politécnico Nacional con material de aprendizaje efectivo, como la guía de estudio del IPN 2024 resuelta.

En esta oportunidad vamos a dar inicio a la solución de los 40 reactivos de cálculo diferencial con los primeros 10 de la guía. Al final de post encuentras las respuestas correctas de cada enunciado, pero no las mires hasta que hayas resuelto el ejercicio por tu cuenta.

Estructura General del Examen

Antes de comenzar el desarrollo de la guía es necesario que conozcas la estructura completa del examen, ya que tiene una duración de tres horas, que debes administrar correctamente para responder 140 reactivos de complejidad variada según el área a la que apliques, las cuales se dividen en:

• IyCFM: Ingeniería y ciencias físico matemáticas.
• CMD: Ciencias médico biológicas.
• CSyA: Ciencias sociales y administrativas.

La prueba comprende dos grandes módulos:

• Conocimientos generales.
• Ciencias experimentales.

El módulo de conocimientos generales engloba las siguientes materias:

• Matemáticas
• Competencia escrita
• Competencia lectora
• Reading comprehension (nuevo tema)
• Historia

Si te fijas, es aquí donde se evalúa el cálculo diferencial, ya que matemáticas pertenece a los conocimientos generales. A diferencia de las ciencias experimentales, en donde solo se evalúa física, biología y química. Y, depende mucho de la carrera a la que apliques. Para que no tengas dudas a continuación tienes una tabla resumen de la estructura de la prueba.

Estructura completa del examen:

Materia	IyCFM	CMB	CSyA
Matemáticas	37	33	35
Competencia escrita	20	20	25
Competencia lectora	20	20	20
Reading comprehension	10	10	10
Historia	10	10	20
Biología	9	17	10
Química	17	17	10
Física	17	13	10

Estructura del nuevo examen de ingreso al instituto Politécnico Nacional 2024.

Cálculo Diferencial de la Guía IPN 2024

¿De qué se trata el cálculo diferencial? Responder esta pregunta puede ser el primer paso para que tengas una comprensión más amplia de cómo resolver cada ejercicio.

En pocas palabras, el cálculo diferencial tiene aplicaciones en muchas áreas porque permite determinar el cambio o la variabilidad de aquello que se analiza. Si pensamos en una gráfica, el cálculo diferencial nos dice qué tan inclinada es la curva en cada punto. Esto es muy útil para encontrar máximos y mínimos, estudiar el movimiento de los objetos, analizar el comportamiento de funciones y muchas otras cosas.

Temario de Cálculo Diferencial

Todo lo que debes estudiar de cálculo diferencial para tu prueba te lo dejamos en esta lista:

• Funciones, límites y continuidad
  • Dominio y rango
  • Desigualdades
  • Definición de límite
  • Teoremas de límites
  • Límites al infinito
  • Continuidad de una función
• Derivada de funciones algebraicas y trascendentes
  • Definición de derivada
  • Interpretación geométrica
  • Fórmulas de derivadas
  • Regla de la cadena
  • Máximos y mínimos

Reactivo 1

Determinar el dominio de la función:

f\left(x\right)=\sqrt{5-x}+\sqrt{3+x}

1. \left[-5, -3\right]
2. \left[3, 5\right]
3. \left[-5, 3\right]
4. \left[-3, 5\right]

Reactivo 2

¿Cuál es el rango de la función?

f\left(x\right)={x}^{2}+4x+12

1. \left[4, \infty \right)
2. \left[8, \infty \right)
3. \left[12, \infty \right)
4. \left[16, \infty \right)

Reactivo 3

Es el dominio de la función:

f\left(x\right)=\mathrm{log}\left(\frac{1+x}{1-x}\right)

1. \left(-\mathrm{1,1}\right)
2. \left[-1, 1\right)
3. \left(0, 1\right)
4. \left[-1, 0\right)

Reactivo 4

Si f\left(x\right)={x}^{2}-2x+1 , determinar el domino de la función:

g\left(x\right)=\frac{f\left(x\right)}{f\left(x\right)-16}

1. \mathfrak{R}-\left\{3, 5\right\}
2. \mathfrak{R}-\left\{-3, 5\right\}
3. \mathfrak{R}-\left\{3,- 5\right\}
4. \mathfrak{R}-\left\{-3, -5\right\}

Reactivo 5

¿Cuántas soluciones enteras tiene la desigualdad?

\sqrt[3]{{x}^{3}-7}<x-1

1. 0
2. 1
3. 2
4. 3

Reactivo 6

Determinar el conjunto solución de la desigualdad:

{x}^{3}+{x}^{2}\le x+1

1. \left(-\infty , 1\right]
2. \left(-\infty , -1\right]
3. \left[1, \infty \right)
4. \left[-1, \infty \right)

Reactivo 7

Determinar el conjunto solución de la desigualdad:

{x}^{2}+\frac{2}{x}<3

1. \left(0, 2\right)
2. \left(0, -2\right)
3. \left(2, 0\right)
4. \left(-2, 0\right)

Reactivo 8

Si el conjunto solución de la desigualdad \left(x+1\right)\left(x-5\right)\ge k es el conjunto \mathfrak{R} , determinar el mayor valor posible de k .

1. -9
2. -4
3. 4
4. 9

Reactivo 9

Calcular el valor del límite:

\underset{x\to 1}{\mathrm{lim}}\left(\frac{1}{1-x}-\frac{3}{1-{x}^{3}}\right)

1. -3
2. -1
3. 1
4. 3

Reactivo 10

La figura muestra la gráfica de una función f\left(x\right) :

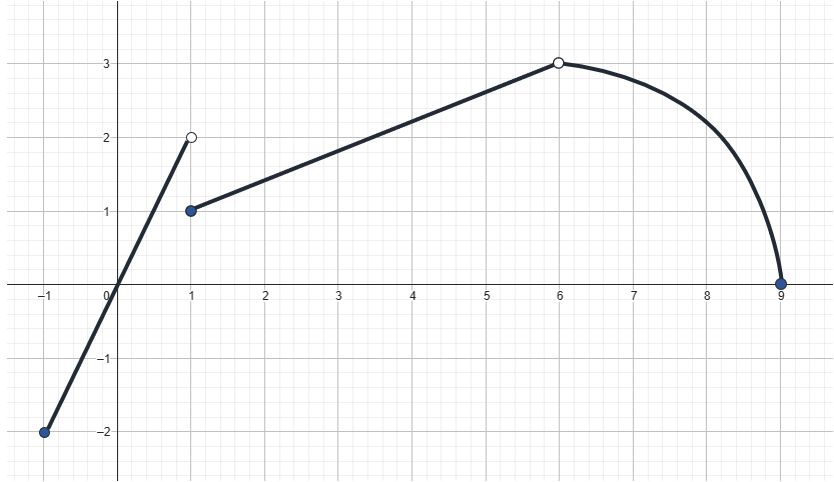
Determinar el valor del límite:

\underset{x\to 1}{\mathrm{lim}}f\left(x\right)

1. 1
2. 2
3. \frac{3}{2}
4. No existe

Respuestas correctas:

1. D
2. B
3. A
4. B
5. C
6. A
7. D
8. A
9. B
10. D