Guía EXANI II Pensamiento matemático | Parte III | del 21 al 30

Antes de continuar con la parte III de la solución de la guía Exani II de ceneval en el área de pensamiento matemático, recuerda que es muy importante que repases todas las áreas de estudio que vienen en el examen de admisión.

Parte I  Parte II

Esto no se acaba aquí, todo lo contrario, si ya identificaste los temas que más se te dificultan te recomiendo profundizar en cada uno de ellos.

Si bien la parte de matemáticas suele ser la que más complicada para muchos aspirantes, existen temas como comprensión lectora y redacción indirecta que requieren en muchos casos de un mayor análisis, no olvides practicar y repasar para mejorar tus habilidades en todas las áreas del examen.

Este es un breve resumen del Exani II:

Estructura del Exani II

Mi recomendación es que comiences por la parte de matemáticas y en paralelo estudies las otras áreas de la estructura del examen de ingreso Exani II.

Recuerda que el nuevo examen de admisión de Ceneval Exani II incluye las siguientes áreas:

Área	Reactivos
Habilidades y conocimientos
Pensamiento matemático	30
Comprensión lectora	30
Redacción indirecta	30
Módulos de conocimientos específicos
Módulo 1	24
Módulo 2	24
Subtotal de reactivos	138
Diagnóstico
Inglés	30
Total de reactivos	168

 Estructura Exani II

Reactivo 21: Problemas matemáticos

Una receta para galletas indica que por cada kilogramo de harina se agregan 420 g de azúcar. La mezcla con el resto de los ingredientes rendirá para 80 galletas. Si se desea reducir a la mitad la cantidad de azúcar para cada galleta, manteniendo la misma cantidad de harina y hay 273 g de azúcar, ¿cuántas galletas se podrán hornear?

1. 26
2. 43
3. 52
4. 104

Solución:

Primero, debemos determinar cuánta azúcar tiene cada galleta con la receta original aplicando una regla de tres directa:

420 \mathrm{~g} \rightarrow 80 \text { galletas }

x \rightarrow 1 \text { galleta }

Nos queda que:

x=\frac{420 \mathrm{~g} \cdot 1 \mathrm{galleta}}{80 \text { galletas }}=5.25 \mathrm{~g}

En la receta original, cada galleta tiene 5.25 \mathrm{~g} de azúcar. Ahora, se desea reducir la cantidad de azúcar a la mitad:

\frac{5.25 g}{2}=2.625 g

Con la nueva receta, cada galleta debe llevar 2.625 gramos de azúcar. Si para dicha nueva receta disponemos de 273 gramos de azúcar ¿Cuántas galletas obtendremos si cada una debe tener 2.625 \mathrm{~g} de azúcar?

\text { galletas }=\frac{273 g}{2.625 g}=104 \text { galletas }

Concluimos escogiendo como respuesta correcta a la opción d).

[wpipa id=»10740″]

Reactivo 22: Problemas matemáticos

Si se requiere de 2 personas para construir una barda de 20 m de largo y 1.5 m de alto en 2 días, ¿cuántas personas se necesitan para construir otra barda igual en medio día?

1. 10
2. 5
3. 8
4. 15

Solución:

Para determinar la cantidad de personas que se necesitan para construir la otra barda en medio día, debemos establecer una relación mediante una regla de tres inversa, pero ¿Por qué inversa?

La regla de tres inversa se emplea cuando una de las cantidades en una relación disminuye cuando la otra aumenta. En este caso, es claro que a medida que la cantidad de empleados aumente el tiempo de fabricación de la barda disminuirá, es una relación inversa.

Regla de tres inversa:

2 \text { días } \rightarrow 2 \text { personas }

\frac{1}{2} \operatorname{dí} a \rightarrow x

x=\frac{2 \text { personas } \cdot 2 \text { días }}{\frac{1}{2} \text { día }}=8 \text { personas }

Se necesitan a 8 personas para terminar la barda en medio día.

Escogemos como respuesta correcta a la opción c).

Reactivo 23: Propiedades de los exponentes

Identifica la ecuación equivalente a la siguiente expresión:

4^{-2} x^{-1} y^{2}

1. \frac{16 y^{2}}{x}
2. -8 x y^{2}
3. -\frac{16 y^{2}}{x}
4. \frac{y^{2}}{16 x}

Solución:

Aplicamos a los factores con potencia negativa la propiedad del exponente negativo:

a^{-n}=\frac{1}{a^{n}}

De esta forma:

4^{-2} x^{-1} y^{2}=\frac{y^{2}}{4^{2} x}

Resolvemos la potencia del 4.

\frac{y^{2}}{4^{2} x}=\frac{y^{2}}{16 x}

Concluimos entonces que:

4^{-2} x^{-1} y^{2}=\frac{y^{2}}{16 x}

Escogemos como respuesta correcta a la opción d).

Reactivo 24: Raíz cuadrada

Calcule la raíz cuadrada de 9 x^{2} y^{6}

1. 3 x y^{4}
2. 3 y^{4}
3. 9 y^{4}
4. 3 x y^{3}

Solución:

Aplicamos raíz cuadrada a todo el monomio.

\sqrt{9 x^{2} y^{6}}

Separamos la raíz como el producto de las raíces de cada uno de los factores del monomio.

\sqrt{9 x^{2} y^{6}}=\sqrt{9} \sqrt{x^{2}} \sqrt{y^{6}}

La raíz cuadrada del 9 es 3, la raíz cuadrada de x^{2} es x y la raíz cuadrada de y^{6} se puede expresar como y^{\frac{6}{2}} .

\sqrt{9} \sqrt{x^{2}} \sqrt{y^{6}}=3 x y^{\frac{6}{2}}

Simplificando nos queda:

\sqrt{9 x^{2} y^{6}}=3 x y^{3}

Comparando con las opciones, escogemos como respuesta correcta a la d).

Reactivo 25: Intersección entre rectas

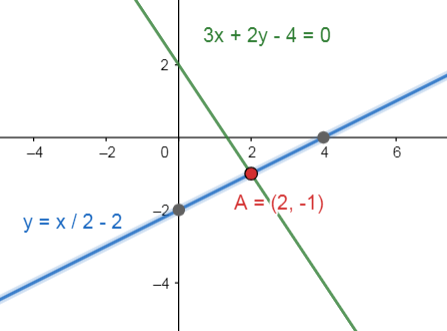
¿Cuál es el punto de intersección entre las rectas?

\begin{array}{c} 3 x+2 y-4=0 \\ y=\left(\frac{x}{2}\right)-2 \end{array}

1. (-2,1)
2. (-1,2)
3. (1,-2)
4. (2,-1)

Solución:

Para encontrar el punto de intersección entre las rectas, debemos resolver el sistema de ecuaciones que forman:

\left\{\begin{array}{c} 3 x+2 y-4=0 \\ y=\left(\frac{x}{2}\right)-2 \end{array}\right.

Se puede aplicar cualquier método de resolución de SEL. Como en la segunda ecuación está la variable y despejada, podemos recurrir directamente al método por sustitución. Sustituimos el valor de y en términos de x en la primera ecuación para encontrar el valor numérico de x .

3 x+2\left[\left(\frac{x}{2}\right)-2\right]-4=0

Simplificamos.

3 x+x-4-4=0

4 x-8=0

Despejamos el valor numérico de x .

4 x=8 \rightarrow x=2

Ahora, se sustituye este resultado en la ecuación y=\left(\frac{x}{2}\right)-2 .

y=\left(\frac{2}{2}\right)-2

Simplificamos.

y=1-2=-1

Concluimos entonces que el punto de intersección entre las rectas es:

(2,-1)

Seleccionamos como respuesta correcta a la opción d).

Reactivo 26: Medidas de localización estadística

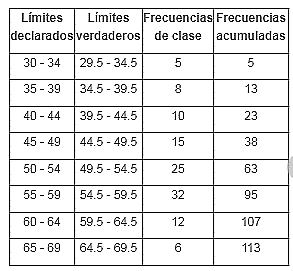
Calcule el primer cuartil de los resultados de un estudio sobre las ventas de coches en una agencia, durante un mes.

1. 47.75
2. 46.25
3. 49.11
4. 49.89

Solución:

Los cuartiles son de tres valores conocidos como medidas de localización, que dividen a un conjunto de datos en 4 subconjuntos cada uno con la misma cantidad de datos. La ecuación para calcular los cuartiles en datos agrupados por intervalo es:

Q_{1}=L_{i}+\frac{\frac{n}{4}-F_{a-1}}{f} \cdot c

Primero, calculamos la posición del intervalo en el que se encuentra el primer cuartil, para ello se utiliza la ecuación de posición para cantidad de intervalos par:

P_{1}=\frac{k n}{4}=\frac{(1)(113)}{4}=28.25

Buscamos en la tabla el intervalo inmediato que tenga una frecuencia acumulada mayor o igual a 28.25, en este caso es el intervalo [44.5,49.5) .

Ahora, sustituimos en la ecuación del primer cuartil:

• L_{i} el límite inferior del intervalo: L_{i}=44.5
• n la frecuencia absoluta total del conjunto de datos: n=113
• F_{a-1} la frecuencia acumulada del intervalo anterior: F_{a-1}=23
• f la frecuencia absoluta de la clase: f=15
• c el ancho de la clase: c=49.5-44.5=5

Sustituimos

Q_{1}=44.5+\frac{\frac{113}{4}-23}{15} \cdot 5=44.5+1.75

Q_{1}=46.25

Comparando con las opciones del problema, escogemos como respuesta correcta a la b).

Reactivo 27: Trigonometría

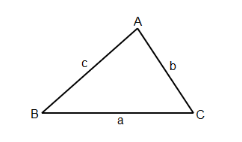
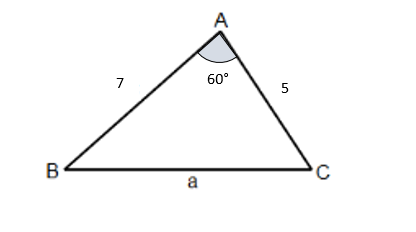
Se va a construir una nueva carretera para comunicar 2 poblaciones: ciudad B y ciudad C. Hasta ahora, para ir de uno a otro poblado es necesario pasar por la ciudad A. La distancia entre la ciudad A y la ciudad B es de 7 km y la distancia entre la ciudad A y la ciudad C es de 5 km. Si el ángulo que forman las 2 carreteras de la ciudad A es de 60°, ¿cuántos kilómetros medirá la nueva carretera?

Considere:

\begin{array}{l} \sin \left(60^{\circ}\right)=0.8660 \\ \cos \left(60^{\circ}\right)=0.5 \\ \tan \left(60^{\circ}\right)=1.7320 \end{array}

1. \sqrt{33}
2. \sqrt{39}
3. \sqrt{72}
4. \sqrt{109}

Solución:

Para calcular la distancia de la carretera entre las ciudades B y C, debemos emplear el teorema del coseno. A partir del triángulo de la imagen, podemos ubicar los datos que tenemos: el ángulo opuesto al lado B C , es decir el ángulo \hat{A} , la distancia del lado A B=7 y la del lado A C=5 .

Según la ley de cosenos:

B C^{2}=A B^{2}+A C^{2}-2|A B \| A C| \cos (\theta)

A B=7, A C=5, \theta=60^{\circ}

Sustituyendo:

B C^{2}=(7)^{2}+(5)^{2}-2(7)(5) \cos \left(60^{\circ}\right)=39

Despejamos y concluimos.

B C=\sqrt{39} \mathrm{~km}

La carretera para unir las ciudades B y C mide \sqrt{39} \mathrm{~km} . Comparando con los incisos, escogemos como respuesta correcta a la opción b).

Reactivo 28: Trigonometría

¿Qué expresión permite calcular el valor del ángulo B?

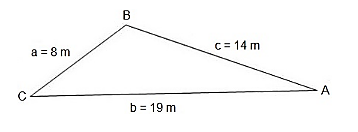
1. Ley de Senos
2. Teorema de Tales
3. Ley de Cosenos
4. Teorema de Pitágoras

Solución:

En el triángulo de la imagen, conocemos el valor de sus tres lados y necesitamos calcular el ángulo que se forma en el vértice B. El teorema de Pitágoras sólo se aplica en triángulos rectángulos, para aplicar el teorema del seno es necesario conocer un ángulo y el teorema de Tales se aplica en problemas con triángulos semejantes.

La ley de cosenos nos permite relacionar los lados de un triángulo con uno de los ángulos, que es opuesto al lado seleccionado. El lado opuesto al ángulo \hat{B} \text { es } C A , por tanto la expresión quedaría:

C A^{2}=B C^{2}+B A^{2}-2|B C \| B A| \cos (\hat{B})

Despejando nos queda:

\cos (\widehat{B})=\frac{B C^{2}+B A^{2}-C A^{2}}{2|B C \| B A|} \rightarrow \hat{B}=\cos ^{-1}\left(\frac{B C^{2}+B A^{2}-C A^{2}}{2|B C \| B A|}\right)

Concluimos entonces que: la ley del coseno nos permitirá calcular el valor del ángulo \widehat{B} .

Seleccionamos como respuesta correcta a la opción c).

Reactivo 29: Trigonometría

Si se conocen los 3 lados de un triángulo oblicuángulo, ¿con qué fórmula se puede calcular el valor de los ángulos?

1. Teorema de Pitágoras
2. Ley de Tangentes
3. Ley de Cosenos
4. Ley de Senos

Solución:

La ley del coseno permite calcular el valor de cualquiera de los ángulos en un triángulo si se conocen sus tres lados. Escogemos como respuesta correcta a la opción c).

Reactivo 30: Operaciones aritméticas

¿Cuál de las siguientes expresiones corresponde a la multiplicación de 9 y un número K?

1. 9-k
2. \frac{k}{9}
3. 9+k
4. 9 k

Solución:

El producto de la constante 9 por la variable k se expresa como:

9 k

Por tanto, seleccionamos como respuesta correcta al inciso d).