¡Hola aspirante! En este tutorial vamos a desarrollar los 30 primeros ejercicios del simulacro de Aritmética correspondiente al módulo 2 del nuevo Exani II de Ceneval.

Aquí puedes ver algunos ítems destacables referentes al Exani II:
- Desarrollo: Ceneval
- Examen de admisión: Exani II
- Reactivos: 168
- Tipo: Opción múltiple
- Duración: 4 horas y media
- Modalidades: Presencial, en línea y desde casa.
Gracias a estos reactivos, podrás simular las condiciones del examen real de EXANI desde tu casa.
A lo largo de este tutorial te daremos algunas recomendaciones que debes seguir durante la solución pero, lo más importante, desarróllalos por tu cuenta antes de mirar las respuestas.
Estructura del Exani II
Para el 2022 la prueba de admisión EXANI II de CENEVAL ha sufrido algunos cambios, estando constituida por dos grandes partes: conocimientos generales, denominada oficialmente como habilidades y conocimientos y otra, correspondiente a los temas de conocimientos específicos que varía según la carrera a la que deseas ingresar.
Conocimientos generales tiene 30 reactivos de matemáticas (distintos a los de aritmética) y otros 60 de español, divididos en partes iguales entre comprensión lectora y redacción indirecta.
También existe un examen diagnóstico de inglés, pero su aplicación depende de tu universidad. Debes consultar dicha información en la web de la institución educativa.
Conoce la estructura de la guía Exani II y del examen de ingreso
| Área | Reactivos |
|---|---|
| Habilidades y conocimientos | |
| Pensamiento matemático | 30 |
| Comprensión lectora | 30 |
| Redacción indirecta | 30 |
| Módulos de conocimientos específicos | |
| Módulo 1 | 24 |
| Módulo 2 | 24 |
| Subtotal de reactivos | 138 |
| Diagnóstico | |
| Inglés | 30 |
| Total de reactivos | 168 |
Estos son los 16 módulos de conocimientos específicos
| 1. Administración | 9. Física |
| 2. Aritmética | 10. Historia |
| 3. Biología | 11. Literatura |
| 4. Cálculo diferencial e integral | 12. Matemáticas financieras |
| 5. Ciencias de la Salud | 13. Premedicina |
| 6. Derecho | 14. Probabilidad y estadística |
| 7. Economía | 15. Química |
| 8. Filosofía | 16. Psicología |
¿Qué tan difícil es el módulo 2 de Aritmética?
Muchos jóvenes que aún no presentan su examen de admisión, suelen preguntar a otras personas con experiencia en estas instancias acerca de la dificultad del Exani II. Sin embargo, la respuesta a esto es algo que solamente tú puedes responderte, ya que dependerá de tus propias condiciones y preparación. Por ello, plantéate las siguientes interrogantes:
- ¿Ya empezaste a estudiar para presentar el examen?
- ¿Le has dedicado suficiente tiempo al estudio de cada módulo de la prueba?
- ¿Consideras que dominas las bases fundamentales en las cuales serás evaluado?
Temario de Aritmética
Aunque pueda parecer confuso que en el examen de admisión haya dos partes muy similares, el módulo de Aritmética en la segunda parte del examen tiene como finalidad comprobar los conocimientos del estudiante en temas como: teoría de números, operaciones y teoría de la divisibilidad.
Los 50 ejercicios que conforman al módulo se distribuyen entre las siguientes ramas de la Aritmética:
| Subárea | Reactivos |
|---|---|
| Principios de números reales | 14 |
| Problemas con números reales | 10 |
| Total | 24 |
Subárea: Principios de números reales
- Operaciones básicas con números enteros, fracciones y decimales
- Ley de los signos
- Potenciación
- Signos de agrupación
- Expresiones algebraicas con radicales
- Notación científica
- Factores primos
- Reglas de divisibilidad
- Mínimo común múltiplo
- Máximo común divisor
Subárea: Problemas con números racionales
- Razón y proporción
- Porcentaje
- Progresión geométrica
- Progresión aritmética
- Reparto proporcional
- Interés simple
- Regla de tres
Puedes encontrar apoyo teórico de estos temas en las referencias bibliográficas al final del módulo de Aritmética en la guía del EXANI II. Aritmética puede parecer una asignatura aburrida, pero es la base del álgebra y la punta de lanza en el análisis de problemas matemáticos.
¿Cómo resolver el examen simulador?
Los ejercicios del simulacro tienen la finalidad de ayudarte a: practicar los temas del examen real y mejorar el tiempo que tardas en resolverlos.
Incluye exámenes simulacro en tu calendario de estudios para cada asignatura, así pondrás en práctica tus conocimientos en condiciones similares a las del examen.
Las siguientes, son sugerencias para tener en cuenta mientras estudias con este simulacro.
- Resuelve completa cada parte por tu cuenta antes de mirar las respuestas
- Establece un tiempo no mayor a 20 minutos por cada 10 reactivos
- Analiza el procedimiento que has seguido para resolver los ejercicios y piensa en posibles alternativas que acorten el tiempo
- Asegúrate de tener unos minutos de sobra para comprobar tus respuestas
- Si un ejercicio parece complejo, ve al siguiente y resuélvelo de último. Lo mejor es mantener la concentración y no entrar en pánico
Reactivo 1
Relacione correctamente la ley de signos con la operación efectuada.
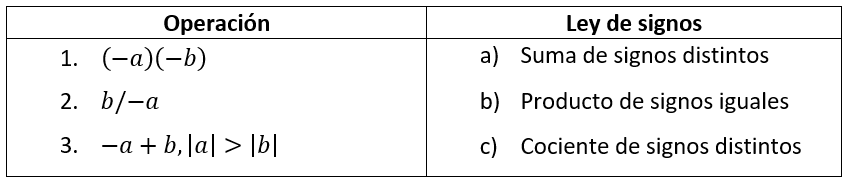
- 1a, 2c, 3b
- 1b, 2c, 3a
- 1a, 2b, 3c
Solución:
Cada caso de la columna izquierda corresponde a un caso de la ley de signos para la suma, división o multiplicación. Es recomendable que tengas muy claras estas leyes de signos antes de continuar con el ejercicio, ya que demostrarlas podría hacer tediosa e innecesariamente larga la solución.
Primera operación.
\left(-a\right)\left(-b\right)
Esta corresponde a un producto o multiplicación, aunque no esté escrito como “*”, “ \bullet ” o “ \times ”, cuando dos cantidades se encuentran una al lado de la otra encerrada entre paréntesis, como en este caso, queda implícita una multiplicación.
Ahora, los signos de ambas cantidades es el mismo, menos para a como para b ; por tanto, se trata de un producto de signos iguales, cuyo resultado es positivo.
\left(-a\right)\left(-b\right)=ab
Indicamos para esta parte: 1b.
Segunda operación.
b/-a
Se trata de un cociente por el símbolo “/”, entre la cantidad b y la cantidad -a . Por una parte, b es positivo y a es negativo; se trata de un cociente de signos distintos, cuyo resultado es negativo según la regla.
\frac{b}{-a}=-\frac{b}{a}
Indicamos que: 2c.
Tercera operación.
Finalmente, vamos con una suma de dos cantidades, una negativa y la otra positiva. Además, se nos indica que el valor absoluto de a es mayor que el valor absoluto de b . Sobre la recta real, ambos valores quedarían representados como:
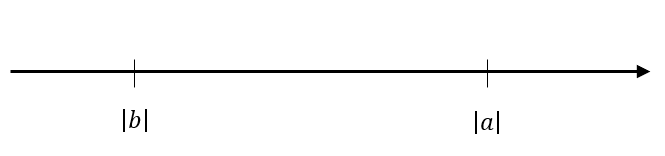
Por esta razón, el resultado de dicha suma será negativo. Concluimos en este caso que: 3a. Uniendo todas las respuestas obtenemos:
1b, 2c, 3a.
Escogemos como respuesta correcta la opción b).
Reactivo 2
Identifique cuál de las siguientes operaciones es incorrecta. Justifique su respuesta indicando la propiedad mal aplicada.
Procedimiento.
-3+\left(3-2\right)-\left(1-3\right)
- -3+\left(1\right)-\left(1-3\right)
- -3+1-\left(-2\right)
- -3+1-2
- -2-2
- 4
- 3 y 5
- 1 y 3
- 2 y 4
Solución:
Para encontrar los pasos en los que se cometió el error, es necesario que desarrollemos el ejercicio por nuestra cuenta. Comencemos recordando que para la suma aplican las siguientes reglas de signos:
- Adición de signos iguales, se suman y se conserva el mismo signo
- Adición de signos opuestos, se restan y se conserva el signo del número con módulo mayor
Además, primero se resuelve lo que se encuentra entre paréntesis y luego se opera el resultado con lo que se encuentra afuera. Iniciamos resolviendo lo que se encuentra en los paréntesis.
-3+\left(3-2\right)-\left(1-3\right)=-3+\left(1\right)-\left(-2\right)
La primera es una resta (suma de signos diferentes), se conserva el signo positivo porque el 3 posee mayor módulo. En la segunda operación, también se efectúa una resta, pero ahora el de módulo mayor es el -3, por tanto, el resultado es negativo. Procedemos a deshacer los paréntesis multiplicando el signo a la izquierda con el signo del número de adentro.
-3+\left(1\right)-\left(-2\right)=-3+1+2
Producto de signos iguales da como resultado positivo y producto de signos diferentes da como resultado negativo. Aquí identificamos un primer error en el paso 2, ya que para el siguiente el +2 se escribe como -2. Finalizamos sumando al -3 con el 1 y dicho resultado sumado luego con el 2.
-3+1+2=-2+2=0
Examinando el cuarto paso del enunciado, se comete otro error al sumar -2 con -2, ya que signos iguales se suman y se conserva el signo y en el paso posterior se ve como se coloca el 4 pero positivo, aunque dicho resultado es incorrecto por el error en el paso 2.
-3+\left(3-2\right)-\left(1-3\right)=0
Concluimos indicando que los pasos con errores son el 2 y el 4. La respuesta correcta es la opción c).
Reactivo 3
¿Cuál es el signo que deberá tener el resultado de la siguiente operación?
\frac{\left(3\right)\left(-2\right)\left(-56\right)\left(4\right)\left(-88\right)\left(5-2\right)\left(7\right)}{\left(2\right)\left(-1\right)\left(\frac{8}{-2}\right)}
- Positivo
- Negativo
- No se puede definir
Solución:
Aunque la expresión parezca intimidante, la verdad es que el enunciado solo nos solicita el signo que debería tener el resultado, pero no el valor numérico propiamente dicho. Teniendo esto en cuenta, procedemos a determinar el signo del numerador, luego el signo del denominador y finalmente aplicamos las propiedades para el signo de un cociente.
Iniciemos por simplificar los factores que parezcan complejos. En el numerador hay una resta entre paréntesis indicada como 5-2 , el resultado de la misma es +3 debido a que el 5 posee mayor módulo.
\frac{\left(3\right)\left(-2\right)\left(-56\right)\left(4\right)\left(-88\right)\left(5-2\right)\left(7\right)}{\left(2\right)\left(-1\right)\left(\frac{8}{-2}\right)}=\frac{\left(3\right)\left(-2\right)\left(-56\right)\left(4\right)\left(-88\right)\left(3\right)\left(7\right)}{\left(2\right)\left(-1\right)\left(\frac{8}{-2}\right)}
En el denominador, tenemos a un cociente de dos cantidades con distinto signo \frac{8}{-2} dividimos y conservamos el signo menos según la regla.
\frac{\left(3\right)\left(-2\right)\left(-56\right)\left(4\right)\left(-88\right)\left(3\right)\left(7\right)}{\left(2\right)\left(-1\right)\left(\frac{8}{-2}\right)}=\frac{\left(3\right)\left(-2\right)\left(-56\right)\left(4\right)\left(-88\right)\left(3\right)\left(7\right)}{\left(2\right)\left(-1\right)\left(-4\right)}
Con todos los factores simplificados, procedemos a obtener el signo en el numerador y en el denominador.
Numerador.
+\bullet -\bullet -\bullet +\bullet -\bullet +\bullet +=-\bullet -\bullet +\bullet -\bullet +\bullet +=+\bullet +\bullet -\bullet +\bullet +=+\bullet -\bullet +\bullet +
=-\bullet +\bullet +=-\bullet +=-
Denominador.
+\bullet -\bullet -=-\bullet -=+
Combinamos.
\frac{-}{+}=-
El resultado deberá ser negativo.
Comparando con las opciones, escogemos como respuesta correcta la b).
Reactivo 4
Determine el signo y el valor que debe tener el número faltante para obtener el resultado final.
-14\bullet \_\_\_\_=28
- -2
- 2
- 7
Solución:
Para encontrar el número faltante, debemos analizar tanto el resultado como su signo. Examinando la operación, nos daremos cuenta que el signo es positivo y, por tratarse de un producto, para que un número negativo multiplicado por otro de resultado positivo, este otro debe ser también negativo.
\left(-\right)\left(-\right)=+
Conociendo el signo, vemos que el resultado es exactamente el doble de 14. No queda dudas que el número faltante en la operación es el -2.
-14\bullet -2=28
Comparando con las opciones, concluimos que la respuesta correcta es la a).
Reactivo 5
La interpretación geométrica de la multiplicación, por ejemplo a\times b , es que tomamos a la cantidad a y la desplazamos en una u otra dirección b veces. ¿Qué determina la dirección del desplazamiento?
- La operación que deseamos realizar
- El valor absoluto de b
- El signo de a y b
Solución:
Como se indica en el enunciado, multiplicar es la forma que encontraron los primeros matemáticos de la historia para resumir una suma continuada de una cantidad por sí misma. Pensemos que 3\times 4 es equivalente a sumar por sí mismo al 3 unas 4 veces.
3\times 4=3+3+3+3=12
Si representamos esta operación en el eje real, es equivalente a iniciar parados en el cero y desplazarnos 4 veces en pasos de 3 unidades hacia la derecha (sentido positivo del eje).
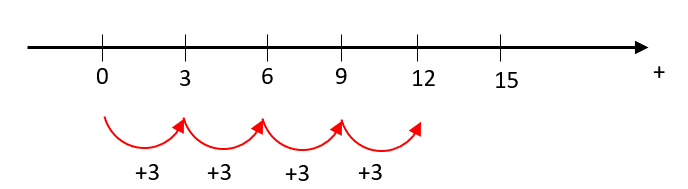
En este caso, el desplazamiento se da en el sentido positivo del eje, pero si cualquiera de las cantidades hubiese sido negativo, el desplazamiento habría sido en sentido negativo. Esto es intuitivo, pero ¿qué sucede cuando ambas cantidades son negativas?
Existen varias maneras de interpretar gráficamente este caso, pero la que te mostraré a continuación me parece la más intuitiva. Si el 3 y el 4 son negativos y se multiplican, uno de ellos puede expresarse como:
-3\times -4=\left(-1\times 3\right)\times -4=-1\times 3\times -4
Consideremos ahora solo la parte 3\times -4 .
-1\times 3\times -4=-1\times (3\times -4)
Expresado sobre el eje de real, sería avanzar en pasos de 3 hacia la izquierda.
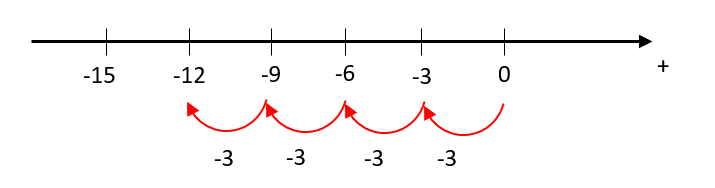
Esto nos da como resultado -12, que ahora debemos multiplicar por -1.
-1\times -12
Esto es equivalente a pararnos en 0 y en lugar de desplazarnos 12 unidades a la izquierda, lo hacemos hacia la derecha debido al signo menos del 1. El signo menos del 1 invierte el sentido impuesto por el menos del 12.
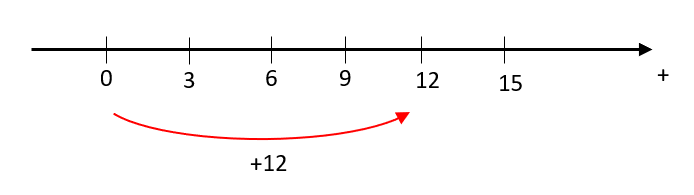
Habiendo examinado todo esto, podemos concluir que: la dirección del desplazamiento queda determinada por los signos de los operandos. Comparando con las opciones, corresponde con la c).
Reactivo 6
Calcule el valor numérico de la siguiente operación.
3-\left(2-5\right)+1-\left[\left(2+3-4\right)-\left(2-7\right)\right]+16
- 16
- 15
- 17
Solución:
Recordando la jerarquía de las operaciones, primero se resuelve lo que está dentro de los corchetes, luego paréntesis y por último lo de afuera. Comencemos por resolver las operaciones dentro de los corchetes.
3-\left(2-5\right)+1-\left[\left(2+3-4\right)-\left(2-7\right)\right]+16=3-\left(2-5\right)+1-\left[\left(1\right)-\left(-5\right)\right]+16
Deshacemos paréntesis.
=3-\left(2-5\right)+1-\left[1+5\right]+16
Resolvemos la suma de distinto signo.
=3-\left(2-5\right)+1-\left[1+5\right]+16=3-\left(2-5\right)+1-\left[6\right]+16
Deshacemos corchetes y resolvemos lo que está entre paréntesis.
=3-\left(2-5\right)+1-\left[6\right]+16=3-\left(-3\right)+1-6+16
Deshacemos el paréntesis.
3-\left(-3\right)+1-6+16=3+3+1-6+16
Finalmente, sumamos y restamos respectivamente.
3+3+1-6+16=6+1-6+16
=7-6+16=1+16
=17
Concluimos indicando que la respuesta correcta es la opción c).
Reactivo 7
Relacione la propiedad con la igualdad correspondiente.

- 1a, 2c, 3b
- 1c, 2a, 3b
- 1a, 2b, 3a
Solución:
Para relacionar correctamente los elementos de una columna con otra, vamos a analizar cada propiedad para luego asociarla con la igualdad correspondiente.
Producto de potencias de igual base.
En este caso, debemos tener en cuenta a dos potencias cuya base será a pero tendrán como exponente 2 y 3 , por ejemplo, respectivamente. El producto de ambas queda como:
{a}^{2}\bullet {a}^{3}
Expandiendo las potencias queda:
\left(a\bullet a\right)\bullet \left(a\bullet a\bullet a\right)=a\bullet a\bullet a\bullet a\bullet a
La potencia se puede reescribir como:
a\bullet a\bullet a\bullet a\bullet a={a}^{5}
Concluimos entonces que, en el producto de potencias de igual base, se mantiene la base y se suman los exponentes.
{a}^{n}\bullet {a}^{m}={a}^{n+m}
Concluimos para este caso: 1a.
Exponente negativo.
Para este caso, iniciamos con la potencia negativa:
{a}^{-n}
Esto lo podemos escribir como:
{a}^{-n}={a}^{0-n}
Si recordamos, una resta de exponentes corresponde a un cociente de potencias.
{a}^{0-n}=\frac{{a}^{0}}{{a}^{n}}
Todo número elevado a cero es la unidad.
\frac{{a}^{0}}{{a}^{n}}=\frac{1}{{a}^{n}}
Finalmente:
{a}^{-n}=\frac{1}{{a}^{n}}
Indicamos para este caso: 2c.
Cociente de radicales con igual radicando.
Una propiedad fundamental que relaciona a las potencias con los radicales, es que estos últimos pueden escribirse como potencias si el índice de la raíz pasa a ser el denominador de una fracción.
\sqrt[n]{a}={a}^{\frac{1}{n}}
Partiendo de acá, podemos escribir el producto de dos radicales como:
\sqrt[n]{a}\bullet \sqrt[m]{a}={a}^{\frac{1}{n}}\bullet {a}^{\frac{1}{m}}={a}^{\frac{1}{n}+\frac{1}{m}}
Decimos entonces: 3b.
Uniendo todas las respuestas obtenemos: 1a, 2c, 3b. Concluimos indicando como correcta la opción a).
Reactivo 8
Encuentre la forma simplificada de la siguiente expresión aplicando las propiedades de los exponentes.
\frac{{3}^{2}\bullet 81+27\bullet 9\bullet 3}{{1253}^{1-\frac{2}{2}}\bullet {3}^{6}}
- 2
- 3
- 1
Solución:
En la gran mayoría de estos ejercicios, debemos identificar una base que es común a todas las potencias que se muestran tanto en el numerador como en el denominador. Podemos sospechar que dicha base es el 3 en este caso, porque el 81, 27 y 9 pueden expresarse como potencias del 3.
9={3}^{2}
27=9\bullet 3={3}^{2}\bullet 3={3}^{3}
81=9\bullet 9={3}^{2}\bullet {3}^{2}={3}^{4}
Sustituimos y simplificamos.
\frac{{3}^{2}\bullet 81+27\bullet 9\bullet 3}{{1253}^{1-\frac{2}{2}}\bullet {3}^{6}}=\frac{{3}^{2}\bullet {3}^{4}+{3}^{3}\bullet {3}^{2}\bullet 3}{{1253}^{1-\frac{2}{2}}\bullet {3}^{6}}=\frac{{3}^{6}+{3}^{6}}{{1253}^{1-\frac{2}{2}}\bullet {3}^{6}}=\frac{2\bullet {3}^{6}}{{1253}^{1-\frac{2}{2}}\bullet {3}^{6}}
Aplicamos la propiedad del cociente de potencias.
\frac{2\bullet {3}^{6}}{{1253}^{1-\frac{2}{2}}\bullet {3}^{6}}=\frac{2\bullet {3}^{6-6}}{{1253}^{1-\frac{2}{2}}}=\frac{2\bullet {3}^{0}}{{1253}^{1-\frac{2}{2}}}=\frac{2\bullet 1}{{1253}^{1-\frac{2}{2}}}=\frac{2}{{1253}^{1-\frac{2}{2}}}
Ahora, exploremos la potencia que hay en el denominador. Tiene como base al 1253 elevado a 1-\frac{2}{2}=1-1=0 , la potencia se puede reescribir como:
\frac{2}{{1253}^{1-\frac{2}{2}}}=\frac{2}{{1253}^{0}}=\frac{2}{1}=2
\frac{{3}^{2}\bullet 81+27\bullet 9\bullet 3}{{1253}^{1-\frac{2}{2}}\bullet {3}^{6}}=2
Finalmente, indicamos como respuesta correcta la opción a).
Reactivo 9
Seleccione el o los pasos en los que se ha cometido error al simplificar la siguiente expresión con exponentes.
\frac{{4}^{3}\bullet {2}^{4}}{4}
- \frac{{4}^{3}\bullet {2}^{4}}{4}=\frac{{\left({2}^{2}\right)}^{3}\bullet {2}^{4}}{{2}^{2}}
- \frac{{\left({2}^{2}\right)}^{3}\bullet {2}^{4}}{{2}^{2}}=\frac{{2}^{5}\bullet {2}^{4}}{{2}^{2}}
- \frac{{2}^{5}\bullet {2}^{4}}{{2}^{2}}=\frac{{2}^{9}}{{2}^{2}}
- \frac{{2}^{9}}{{2}^{2}}={2}^{7}
- 1
- 1 y 2
- 2
Solución:
Como es debido en este tipo de problemas, es necesario que resolvamos el ejercicio por nuestra cuenta para identificar cual o cuales son los pasos en los que se ha cometido un error. Observando las bases de las potencias, nos daremos cuenta que todas pueden expresarse con base 2, por lo que pasamos a transformar a dichos factores.
\frac{{4}^{3}\bullet {2}^{4}}{4}=\frac{{\left({2}^{2}\right)}^{3}\bullet {2}^{4}}{{2}^{2}}
Para el factor del numerador, aplicamos potencia de una potencia.
{\left({a}^{n}\right)}^{m}={a}^{n\bullet m}\to \frac{{\left({2}^{2}\right)}^{3}\bullet {2}^{4}}{{2}^{2}}=\frac{{2}^{6}\bullet {2}^{4}}{{2}^{2}}
Aquí identificamos el primer error en la solución del enunciado. En el paso 2 se suma al 3 con el 2, pero en realidad había que multiplicarlos. Continuamos.
\frac{{2}^{6}\bullet {2}^{4}}{{2}^{2}}=\frac{{2}^{10}}{{2}^{2}}={2}^{8}
Concluimos que se cometió un error en el paso 2 al aplicar la propiedad potencia de una potencia. La respuesta correcta es la opción c).
Reactivo 10
¿Cuál es el resultado de simplificar la siguiente expresión con potencias?
\frac{{m}^{5}\bullet {m}^{\frac{3}{2}}}{{\left({m}^{13}\right)}^{\frac{1}{2}}}
- 2
- 1
- 1/4
Solución:
Debemos aplicar sistemáticamente las propiedades de producto y división de potencias hasta llegar a la expresión más resumida posible. Comencemos por el numerador.
\frac{{m}^{5}\bullet {m}^{\frac{3}{2}}}{{\left({m}^{13}\right)}^{\frac{1}{2}}}=\frac{{m}^{5+\frac{3}{2}}}{{\left({m}^{13}\right)}^{\frac{1}{2}}}=\frac{{m}^{\frac{13}{2}}}{{\left({m}^{13}\right)}^{\frac{1}{2}}}
Aplicamos potencia de una potencia al denominador.
\frac{{m}^{\frac{13}{2}}}{{\left({m}^{13}\right)}^{\frac{1}{2}}}=\frac{{m}^{\frac{13}{2}}}{{m}^{13\bullet \frac{1}{2}}}=\frac{{m}^{\frac{13}{2}}}{{m}^{\frac{13}{2}}}
Simplificamos.
\frac{{m}^{\frac{13}{2}}}{{m}^{\frac{13}{2}}}={m}^{\frac{13}{2}-\frac{13}{2}}={m}^{0}=1
Finalmente:
\frac{{m}^{5}\bullet {m}^{\frac{3}{2}}}{{\left({m}^{13}\right)}^{\frac{1}{2}}}=1
Concluimos seleccionando la opción b) como respuesta correcta.
Reactivo 11
Un tanque se llena a razón de 4 L por minuto. Si originalmente tenía 133 L, ¿cuántos litros tendrá a los 5 minutos?
- 20
- 113
- 153
Solución:
Tenemos un volumen inicial de 133 L y que se llena a una razón de 4 L por minuto. Para calcular el volumen en un determinado instante de tiempo, debemos sumar a los 133 L el resultado de multiplicar 4 L/min por el tiempo transcurrido, es decir 5 minutos.
V_{f}=133 L+4 \frac{L}{\min } \cdot(5 \min )
Se simplifica minutos con minutos y quedan 4*5 L.
V_{f}=133 L+20 L=153 L
Concluimos que, transcurridos 5 minutos el tanque tendrá un volumen de 153 litros. Comparando el resultado con las opciones del problema, la respuesta correcta es la C.
Reactivo 12
Carlos y Juan tienen $116 para gastar en la kermés de su escuela. Si la entrada les costó $10 por persona y gastaron $45 más entre los 2, ¿cuánto dinero les quedó?
- $51
- $61
- $71
Solución:
En un principio, Carlos y Juan tenían 116 pesos, para pagar las entradas gastaron un total de 20 pesos y luego 45 pesos más entre los dos. Dicho de otra forma, a 116 pesos se le restan 20 pesos y luego 45.
\$ 116-\$ 20-\$ 45=\$ 51
Concluimos que a Carlos y Juan les queda $51 luego de asistir a la kermes de su escuela. Se escoge como respuesta correcta a la opción a).
Reactivo 13
Para realizar una práctica de Química cada alumno de un grupo necesita 3 tubos de ensayo para reacciones y 4 para la identificación del pH. En el grupo hay 6 equipos formados por 4 alumnos cada uno. Si el día de la práctica faltaron 3 alumnos, ¿cuántos tubos de ensayo se utilizaron?
- 119
- 147
- 165
Solución:
En total, cada estudiante necesita 7 tubos de ensayo (3 para reacciones y 4 para identificación del pH). Además, el número total de estudiantes que deben asistir al laboratorio es 6 \cdot 4=24 , si el día de la práctica no asisten 3 el total cambia a 24-3=21 estudiantes.
El número total de tubos de ensayo utilizados se obtiene multiplicando 7 por la cantidad de estudiantes que asistieron al laboratorio ese día, es decir 21 por tanto:
7 \cdot 21=147
Se emplearon 147 tubos de ensayo. Comparando con las opciones, escogemos como respuesta correcta a la b).
Reactivo 14
A un evento de 2 días acuden 11 grupos de personas. Si el primer día se presentaron 2 grupos por la mañana, 2 en la tarde y 2 en la noche, ¿cuántas personas acudieron el segundo día? Considere que un grupo se integra por 4 autobuses con 40 pasajeros cada uno.
- 320
- 480
- 800
Solución:
Para calcular la cantidad de personas que asistieron el segundo día, debemos analizar lo que dice el enunciado con detenimiento. Sabemos que el evento tendrá una duración de 2 días y que van a asistir 11 grupos de personas. Además, durante el primer día asistieron:
2 \text { mañana }+2 \text { tarde }+2 \text { noche }=6 \text { grupos }
Por tanto, para el segundo día quedan:
11-6=5 \text { grupos }
Ahora, solo nos queda conocer cuántas personas hay por grupo, para multiplicar ese número por los 5 grupos que asistieron el segundo día. Un grupo está compuesto por 4 autobuses de 40 personas, es decir:
4 \text { autobuses } \cdot 40 \text { personas }=160 \text { personas }
El segundo día asistió un total de:
5 \text { grupos } \cdot 160 \text { personas }=800 \text { personas }
Comparando nuestro resultado con las opciones, escogemos como respuesta correcta a la c).
Reactivo 15
Cinco hermanos recibieron en partes iguales una herencia de $8,575 pesos y a cada uno se le retuvieron $525 pesos por concepto de impuestos. ¿Qué cantidad neta recibió cada hermano?
- $1,180
- $1,190
- $1,620
Solución:
Si cada hermano recibió la misma cantidad de dinero, el total sin retención de impuestos fue:
\frac{\$ 8,575}{5}=\$ 1,715
Ahora, debemos restar la retención por concepto de impuestos al resultado anterior:
\$ 1,715-\$ 525=\$ 1,190
Cada hermano obtuvo un total de $1,190 de la herencia luego de pagar impuestos. Comparando nuestro resultado con las opciones del problema, la respuesta correcta es la b).
Reactivo 16
¿Cuál es el valor de un medio de dos tercios de tres cuartos de cuatro quintos de cinco sextos de seis séptimos de siete octavos de ocho novenos de nueve décimos de 1,000?
- 1/10
- 1
- 100
Solución:
Debemos comenzar por el final, multiplicando la fracción nueve décimos por 1,000 y el resultado por la fracción anterior y así sucesivamente hasta llegar a la primera.
… nueve décimos de 1,000
\frac{9}{10} \cdot 1,000=900
…ocho novenos de…
\frac{8}{9} \cdot 900=800
…siete octavos de…
\frac{7}{8} \cdot 800=700
…seis séptimos de…
\frac{6}{7} \cdot 700=600
…cinco sextos de…
\frac{5}{6} \cdot 600=500
…cuatro quintos de…
\frac{4}{5} \cdot 500=400
…tres cuartos de…
\frac{3}{4} \cdot 400=300
…dos tercios de…
\frac{2}{3} \cdot 300=200
…un medio de…
\frac{1}{2} \cdot 200=100
Comparando nuestro resultado con las opciones del problema, seleccionamos como respuesta correcta a la opción C).
Reactivo 17
En una caja hay 450 canicas, 2/5 partes son azules, el resto son rojas y amarillas en la misma cantidad, ¿cuántas canicas rojas hay en la caja?
- 135
- 150
- 180
Solución:
La cantidad de canicas azules de obtiene multiplicando la proporción 2/5 por el total de canicas en la caja:
450 \cdot \frac{2}{5}=180
Hay 180 canicas azules, es decir que 450-180=270 son rojas y amarillas. Ya que hay la misma cantidad de canicas rojas que amarillas, obtenemos el total de las rojas dividiendo 270 entre 2:
\text { canicas rojas }=\frac{270}{2}=135
Concluimos entonces que en la caja hay 135 canicas rojas. Comparando con las opciones, escogemos como respuesta correcta a la opción a).
Reactivo 18
Resuelva el ejercicio respetando el orden de las operaciones.
32525-123725 \div 49
- -91200.00
- -1861.22
- 30000.00
Solución:
Debemos recordar el orden en el que se resuelven las operaciones aritméticas:
- Paréntesis
- Multiplicaciones y divisiones
- Sumas y restas
En este caso no hay paréntesis, primero se resuelve la división y luego la resta.
32525-123725 \div 49=32525-2525
Restamos.
32525-2525=30000
Comparando con las opciones, se escoge como respuesta correcta a la opción C).
Reactivo 19
En un videojuego, Martha ganó 17 juegos y acumuló 14,450 puntos. Si en cada juego ganó el mismo número de puntos, ¿cuántos obtuvo en cada uno?
- 791
- 802
- 850
Solución:
Para obtener la cantidad de puntos por juego, debemos dividir los 14,450 puntos totales entre las 17 partidas.
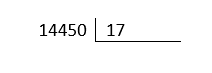
Intentamos con el 8.
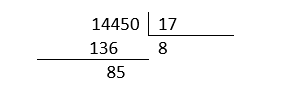
Intentamos con el 50.
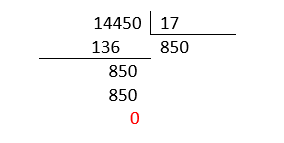
Concluimos que hizo un total de 850 puntos por juego. Escogemos como respuesta correcta a la opción c).
Reactivo 20
Una persona tenía en su tarjeta $5,550 y realizó un pago de $1,595. ¿Cuánto le queda?
- $3,955
- $4,055
- $6,935
Solución:
Para calcular el saldo que queda en la tarjeta, solo debemos restar al monto inicial de $5,550 la cantidad que ha gastado $1,595.
\$ 5,550-\$ 1,595=\$ 3,955
Quedan en su tarjeta $3,955. Escogemos como respuesta correcta a la opción a).
Reactivo 21
Determine el resultado de sumar nueve séptimos a cuatro quintos.
- \frac{73}{35}
- \frac{13}{35}
- \frac{13}{12}
Solución:
Para obtener el resultado de la suma, debemos aplicar la regla del producto cruzado:
\frac{a}{b}+\frac{c}{d}=\frac{a \cdot d+b \cdot c}{b \cdot d}
La primera fracción es \frac{9}{7} y la segunda \frac{4}{5} .
\frac{9}{7}+\frac{4}{5}=\frac{9 \cdot 5+7 \cdot 4}{7 \cdot 5}=\frac{45+28}{35}=\frac{73}{35}
Comparando con las opciones, escogemos como respuesta correcta la a). Otra forma de sumar fracciones es aplicando MCM, pero en este caso no es necesario porque solo hay 2 fracciones.
Reactivo 22
Javier fue contratado para pintar la pared de un negocio. El primer día terminó \frac{2}{9} de la misma y su amigo Luis le ayudó con \frac{1}{7} , sin embargo, pasó un coche y roció con agua lodo \frac{1}{10} de la pared, justo en un área que acababa de terminar, por lo que su jefe le pidió que volviera a trabajar en ella ¿Qué tanto le falta por pintar?
- \frac{2}{3}
- \frac{38}{315}
- \frac{463}{630}
Solución:
El primer día Javier y Luis pintaron un total de \frac{2}{9}+\frac{1}{7} de la pared, es decir:
\frac{2}{9}+\frac{1}{7}=\frac{14+9}{63}=\frac{23}{63}
Pero el coche roció \frac{1}{10} partes recién pintadas con agua y lodo, esto hizo que la porción de pared pintada disminuyera a:
\frac{23}{63}-\frac{1}{10}=\frac{230-63}{630}=\frac{167}{630}
Por último, podemos calcular cuánto les falta por pintar luego de que el coche rociara la pared restándole \frac{167}{630} a 1:
1-\frac{167}{630}=\frac{463}{630}
Concluimos que a Javier le falta por pintar \frac{463}{630} de la pared. Comparando, escogemos como respuesta correcta a la opción c).
Reactivo 23
Julia tiene una computadora cuyo disco duro está casi lleno, puesto que \frac{1}{3} de su capacidad está dedicada a fotos y videos, \frac{2}{7} a archivos y \frac{1}{8} a la información de los programas que instalo. Si compra \frac{2}{3} más de memoria, ¿cuánto espacio disponible habrá?
- \frac{5}{168}
- \frac{155}{168}
- \frac{43}{45}
Solución:
Para calcular la memoria libre que tendrá Julia luego de ampliar su disco, debemos determinar primero cuánta memoria tiene ocupada en este momento.
\text { Espacio ocupado }=\frac{1}{3}+\frac{2}{7}+\frac{1}{8}=\frac{125}{168}
Ahora, Julia compró un disco que tiene \frac{2}{3} de memoria adicional a su espacio actual, es decir:
\text { Espacio nuevo }=1+\frac{2}{3}=\frac{5}{3}
Por tanto, el espacio libre que tiene Julia ahora se obtiene al restar del espacio nuevo el espacio ocupado:
\text { Espacio libre }=\frac{5}{3}-\frac{125}{168}=\frac{155}{168}
Comparando con las opciones del problema, seleccionamos como respuesta correcta a la opción b).
Reactivo 24
En un despacho se organiza una comida con el personal para celebrar el día del abogado; es tradición que cada uno de los tres jefes paga \frac{1}{5} del monto total del evento y el resto lo pagan entre los 12 empleados restantes. Sí este año el costo del evento es de $5,250 pesos, ¿cuánto debe pagar cada empleado?
- 87 \frac{1}{2}
- 175
- 233
Solución:
Ya que los 3 jefes deben pagar \frac{1}{5} parte del evento, la contribución total de ellos cancelaría \frac{3}{5} partes de los $5,250 pesos, es decir \$ 5,250 \cdot \frac{3}{5}=\$ 3,150 pesos.
A los 12 empleados les toca pagar el resto:
\$ 5,250-\$ 3,150=\$ 2,100
Si la deuda se reparte en partes iguales, a cada uno de ellos le tocaría pagar:
\frac{\$ 2,100}{12}=\$ 175
Comparando con las opciones, la respuesta correcta es la b).
Reactivo 25
Se desea envasar \frac{23}{7} L de perfume en frascos con capacidad de \frac{1}{8} L. ¿Cuántos frascos se requerirán?
- \frac{7}{184}
- \frac{23}{56}
- \frac{184}{7}
Solución:
Para calcular la cantidad de frascos que se necesitan, debemos dividir el volumen total de perfume a envasar: \frac{23}{7} L entre la capacidad de un frasco: \frac{1}{8} L.
N^{\circ} \text { de } f r a s c o s=\frac{\frac{23}{7}}{\frac{1}{8}}=\frac{184}{7}
Se necesitan \frac{184}{7} o 26.28 frascos para envasar el volumen total de perfume. Comparando con las opciones, la respuesta correcta es la c).
Reactivo 26
Si a un niño de 2 años se le debe suministrar 1 \frac{1}{4} ml de un medicamento, ¿Qué cantidad se le deberá recetar a un niño de 12 años y 4 meses si la cantidad aumenta proporcionalmente de acuerdo a la edad del paciente?
- 4 \frac{14}{15}
- 6 \frac{1}{24}
- 7 \frac{17}{24}
Solución:
De este problema podemos identificar algunos detalles. Primero, una de las fracciones está en forma mixta y para facilitar la solución debemos convertirla a una fracción impropia. Segundo, el enunciado indica que la proporción es directa, por lo que aplicamos una regla de tres directa.
1 \frac{1}{4}=1+\frac{1}{4}=\frac{5}{4} m l
La edad del segundo niño está en año y meses, mientras que la otra edad está solo en años. Tenemos dos opciones: convertimos ambas a meses o expresamos a la segunda solo en años. Como la segunda opción implica una sola transformación esa será nuestra elección.
Si 12 meses son 1 año, 4 meses cuantos años son:
x=\frac{4 \text { meses } \cdot 1 \text { año }}{12 \text { meses }}=\frac{1}{3} a \text { ño }
Este resultado lo sumamos a los 12 años:
12+\frac{1}{3}=\frac{37}{3} a \text { ños }
Con todas las unidades expresadas de la misma forma y con solo fracciones impropias, pasamos a establecer la regla de tres directa:
2 \text { años } \rightarrow \frac{5}{4} m l
\frac{37}{3} a \text { ños } \rightarrow x
x=\frac{\frac{5}{4} \cdot \frac{37}{3}}{2}=\frac{185}{24} m l
Como todas las respuestas están escritas en forma de fracción mixta, convertimos nuestro resultado a fracción mixta:
\frac{185}{24} m l=7 \frac{17}{24} m l
Se deben aplicar 7 \frac{17}{24} m l de medicamento a un niño de 12 años y 4 meses. Comparando con las opciones, la respuesta correcta es la c).
Reactivo 27
La mamá de Lupita prepara nieve y una vez que está lista la reparte en porciones iguales a los 5 miembros de la familia, tocándole a cada uno \frac{2}{15} de litro. Si Lupita invita a algunos amigos a tomar nieve y su mamá tiene que repartirla en 15 porciones iguales, ¿qué cantidad le toca a cada uno?
- \frac{1}{18}
- \frac{2}{45}
- \frac{24}{25}
Solución:
Antes de la inesperada llegada de los amigos de Lupita, la nueve se dividió en 5 porciones de \frac{2}{15} de litro, es decir en \frac{10}{15} \text{ o } \frac{2}{3} en total. Repentinamente, llegan 10 amigos de Lupita a casa, por lo que su mamá ahora debe repartir la nieve entre 15 personas.
Para calcular cuanta porción de nieve le queda a cada uno, se dividen los litros servidos con anterioridad, es decir \frac{2}{3} entre la nueva cantidad de personas 15.
\frac{\frac{2}{3}}{15}=\frac{2}{45}
Ahora, cada porción será de \frac{2}{45} litros. Finalmente, escogemos como respuesta correcta a la opción b).
Reactivo 28
Un fabricante de pantalones paga a sus trabajadores según el trabajo realizado. Si paga $12,000 por elaborar 150 pantalones, ¿cuántos pantalones es necesario elaborar para recibir $18,000?
- 100
- 210
- 225
Solución:
En este caso, debemos establecer una regla de tres para encontrar la respuesta correcta. Ahora, tenemos dos opciones: la regla de tres directa y la regla de tres inversa, para escoger una de ellas debemos identificar si la relación entre las cantidades es directa o inversa.
Basados en el contexto del problema, es claro que mientras más pantalones elaboren los empleados mayor será el pago final, por tanto la relación entre variables de directa.
Regla de tres directa.
\$ 12,000 \rightarrow 150 \text { pantalones }
\$ 18,000 \rightarrow x
x=\frac{\$ 18,000 \cdot 150 \text { pantalones }}{\$ 12,000}=225 \text { pantalones }
Concluimos entonces que: para recibir $18,000 un empleado debe hacer 225 pantalones. Comparando con las opciones, la respuesta correcta es la c).
Reactivo 29
Para elaborar una alfombra de 200 \mathrm{~m}^{2} se requiere de 8 artesanos durante 20 días. Si únicamente trabajan 6 artesanos, ¿cuántos metros de alfombra podrán elaborar en 12 días?
- 90
- 120
- 160
Solución:
En este caso, debemos establecer una regla de tres mixta o múltiple, porque la relación se da entre 3 cantidades y no 2 como sucede en la regla de tres simple.
8 \text { artesanos } \rightarrow 20 \text { días } \rightarrow 200 \mathrm{~m}^{2}
6 \text { artesanos } \rightarrow 12 \text { días } \rightarrow x \mathrm{~m}^{2}
Ahora, identificamos si la relación entre la cantidad incógnita y las otras dos es directa o inversa.
Relación metros cuadrados de alfombra y cantidad de artesanos, es una relación directa porque a mayor cantidad de artesanos más metros cuadrados se pueden tejer.
Relación metros cuadrados de alfombra y días transcurridos, mientras más tiempo se mantenga un grupo de artesanos tejiendo, mayor será la cantidad de metros cuadrados, por tanto la relación es directa.
Finalmente, escribimos la fracción \frac{200}{x} igualada al producto de \frac{8}{6} \text{ y } \frac{20}{12} .
\frac{200}{x}=\left(\frac{8}{6}\right) \cdot\left(\frac{20}{12}\right)
Resolvemos el producto de fracciones.
\frac{200}{x}=\frac{20}{9}
Despejamos a x .
x=\frac{200 \cdot 9}{20}=90
Comparando nuestro resultado con las opciones del problema, escogemos a la a) como la correcta.
Reactivo 30
Si 58 es el 29% de una cantidad, el 16% de esa misma cantidad es:
- 13
- 26
- 32
Solución:
Tenemos diferentes vías para resolver este problema, por definición de porcentaje o por regla de tres. Debido a que es más corto y sencillo de entender, lo haremos por regla de tres, en este caso directa porque el porcentaje es una relación directa.
Decimos que:
\begin{array}{l} 29 \% \rightarrow 58 \\ 16 \% \rightarrow x \end{array}
x=16 \% \cdot \frac{58}{29 \%}=32
Concluimos que: el 16% de una cierta cantidad es igual a 32. Comparando con las opciones, la respuesta correcta es la c).
Reactivo Extra
Si un artículo cuesta 100 pesos más 15% de IVA, pero tiene un descuento del 15% calculado sobre el precio con IVA incluido, ¿cuál es el precio final del producto?
- 100
- 75
- 25
Solución:
Primero, calculamos el precio del artículo con el IVA incluido y a ese resultado le aplicamos un descuento del 15% porque el enunciado indica que dicho descuento se aplica al precio del artículo con el IVA incluido.
\text { Precio con IVA }=\$ 100 * 1.15=\$ 115
\text { Precio con descuento }=\$ 115 * 0.85=\$ 97.75
El cliente deberá pagar $97.75 por el producto. Comparando con las opciones, escogemos como respuesta correcta a la opción b).
Reactivo Extra
En un taller de costura se han fabricado 1 000 camisas trabajando 8 horas diarias durante 5 días. Si se trabajan 10 horas diarias, ¿en cuántos días se fabricarán 2 000 camisas?
- 2
- 3.1
- 8
Solución:
Este problema se resuelve aplicando una regla de tres compuesta. Primero, identificamos las cantidades en juego: camisas, horas y días. Además, la cantidad desconocida son días, por tanto se coloca más hacia la derecha.
Pasamos a ordenar los datos suministrados.
1000 \text { camisas } \rightarrow 8 \text { horas } \rightarrow 5 \text { dias }
2000 \text { camisas } \rightarrow 10 \text { horas } \rightarrow x \text { días }
Ahora, establecemos si la relación entre días-camisas y días-horas es directa o inversa. Es claro que mientras más días trabaje, mayor será el número de camisas. Por otro lado, mientras más horas por día se trabajan menos días se necesitan para culminar una x cantidad de camisas, por tanto es inversa.
Procedemos finalmente a plantear la regla de tres compuesta, directa para la cantidad de camisas e inversa para las horas:
\frac{5}{x}=\frac{1000}{2000} \cdot \frac{10}{8}=\frac{5}{8}
Despejamos a x .
x=8
Concluimos entonces que: con 10 horas diarias se necesitan 8 días de trabajo para culminar 2 000 camisas. Comparando con las opciones, la respuesta correcta es la c).

