¡Muy bien aspirante! Llegamos a la tercera y última parte del simulacro resuelto de Probabilidad y Estadística para la prueba de ingreso EXANI II. Pasamos con la solución de los reactivos del 41 al 50.

Recuerda tomar descansos de 20 minutos al terminar cada parte del simulacro. Un rato lejos de los libros y los reactivos te ayudará a pensar mejor.
Ejercicios de Probabilidad y Estadística
Finalmente, vamos con la última parte de este simulacro. En UnibetasPro puedes encontrar más simulacros como este, totalmente gratuitos y diseñados para que marques el inicio de tu mayor meta.
Reactivo 41
Indique cual o cuales de las siguientes oraciones es incorrecta.
- La probabilidad del inverso de un suceso es igual a 1 menos la probabilidad del suceso
- Un suceso imposible es aquel que tiene probabilidad muy chica pero no cero
- La sumatoria de las probabilidades de los sucesos es igual a 1
- 2
- 1
- 4
Solución:
Para encontrar la o las frases que enuncian algo incorrecto, debemos analizar una a una teniendo en cuenta los conceptos básicos sobre probabilidades.
La probabilidad del inverso de un suceso es igual a 1 menos la probabilidad del suceso.
En efecto, esta es una de las principales consecuencias de los axiomas de las probabilidades. La probabilidad del opuesto de un evento será igual a la probabilidad del resto de eventos, es decir, el total menos P\left(A\right) .
P\left(\stackrel{-}{A}\right)=1-P\left(A\right)
Un suceso imposible es aquel que tiene probabilidad muy baja pero no cero.
Si la probabilidad es una magnitud que cuantifica de cero a 1 cuán posible es que un evento ocurra, sale de manera natural asociar que una probabilidad igual a cero indica imposible dicho suceso y que si es 1 el evento ocurrirá con total seguridad.
P\left(\varnothing \right)=0
Esta aseveración es falsa.
La sumatoria de las probabilidades de los sucesos es igual a 1.
Si un experimento aleatorio puede tener N posibles estados, entonces la probabilidad del evento {n}_{i} será:
P\left({n}_{i}\right)=\frac{{n}_{i}}{N}
Ahora, si sumamos las i ésimas probabilidades:
P\left(U\right)=\frac{{n}_{1}}{N}+\dots +\frac{{n}_{i}}{N}=\frac{{n}_{1}+\dots +{n}_{i}}{N}
Si el total de los eventos es N , la suma de todos los eventos se puede reemplazar como:
P\left(U\right)=\frac{{n}_{1}+\dots +{n}_{i}}{N}=\frac{N}{N}=1
Esta frase es correcta.
Concluimos comparando con las opciones, e indicamos como correcta la a).
Reactivo 42
La línea de producción de una compañía disquera ha determinado luego de un estudio estadístico que por cada 1000 discos que copia, unos 75 de ellos salen con errores que los vuelven inutilizables.
¿Cuál es la probabilidad de que la máquina haga una buena copia?
- 0.925
- 0.075
- 1
Solución:
Para calcular la probabilidad de un evento, debemos aplicar la definición clásica de Laplace:
P\left(A\right)=\frac{n}{N}
Donde:
- n es el número de casos favorables al evento A
- N es el total de casos posibles del experimento
Necesitamos la probabilidad de una buena copia, pero tenemos el número de copias defectuosas, podemos hacer una de dos cosas:
- Calcular el número de sucesos relacionados con copias buenas
- Calcular la probabilidad de copias defectuosas y luego aplicar la probabilidad del suceso contrario
Aplicaremos la segunda. Hay que destacar que en este caso se puede emplear porque solo hay dos posibilidades: bueno o malo, si hubiese más tendríamos que analizar el problema de otra forma.
DB=1000-DM=1000-75=925
P\left(DB\right)=\frac{925}{1000}=0.925
Comparando con las opciones, la respuesta correcta es la a).
Reactivo 43
Se escriben al azar las 5 vocales. ¿Cuál es la probabilidad de que la “e” aparece de primera y la “o” de última?
Nota: no hay repetición de las letras.
- \frac{1}{2}
- \frac{1}{20}
- \frac{1}{5}
Solución:
Ya que el enunciado limita las posibles formas de ordenar las vocales, indicando que las mismas no se pueden repetir, solo nos queda calcular dos cosas para sustituir en la fórmula de probabilidad:
- Las formas de ordenar las 5 vocales sin repetición
- Las formas de ordenar la a, i, u manteniendo fijas a la e y la o
Ya que intervienen todos los elementos en ambos casos e importa el orden, aplicamos la fórmula de permutación:
{P}_{m}=m!
El total de las 5 vocales.
{P}_{5}=5!=120
El total de las 3 vocales centrales.
{P}_{3}=3!=6
Finalmente:
P\left(A\right)=\frac{6}{120}=\frac{1}{20}
Comparando con las opciones, la respuesta correcta está en la b).
Reactivo 44
Un estudiante de mecatrónica solo ha estudiado 20 de los 30 temas que van para su examen de electrónica aplicada. En dicha prueba, se deben contestar las preguntas de 2 temas extraídos al azar.
Calcule la probabilidad de que los temas que salgan sean de los que estudió el joven.
- 0.4
- 0.41
- 0.43
Solución:
Primero debemos identificar cómo se relacionan los eventos de contestar correctamente a cada uno de los dos temas seleccionados al azar. Si pensamos, la extracción del segundo tema {A}_{2} depende del tema que se haya extraído primero, es decir, {A}_{1}
Por tanto, debemos calcular la probabilidad de la intersección de dos sucesos dependientes.
P\left({A}_{1}\cap {A}_{2}\right)=P\left({A}_{1}\right)\bullet P\left({A}_{2}/{A}_{1}\right)
La probabilidad de extraer un primer tema de los que estudió el alumno es:
P\left({A}_{1}\right)=\frac{20}{30}
Ahora, solo quedan 19 temas de los 20 que estudio y en total restan 29.
P\left({A}_{2}/{A}_{1}\right)=\frac{19}{29}
P\left({A}_{1}\cap {A}_{2}\right)=\left(\frac{2}{3}\right)\left(\frac{19}{29}\right)=0.43
La probabilidad de que salgan solo temas que estudió el alumno es del 43%.
Comparando con las opciones, la correcta está en la c).
Reactivo 45
En un concurso se tienen dos cajas, la primera posee 4 bolas blancas y 3 bolas verdes y en la segunda 2 blancas y 5 rojas. ¿Cuál es la probabilidad de extraer una bola blanca al seleccionar aleatoriamente una de las dos cajas?
- \frac{3}{7}
- \frac{1}{7}
- \frac{2}{8}
Solución:
Este tipo de problemas con probabilidad compuesta pueden visualizarse mejor si se realiza el diagrama de árbol de la situación planteada.
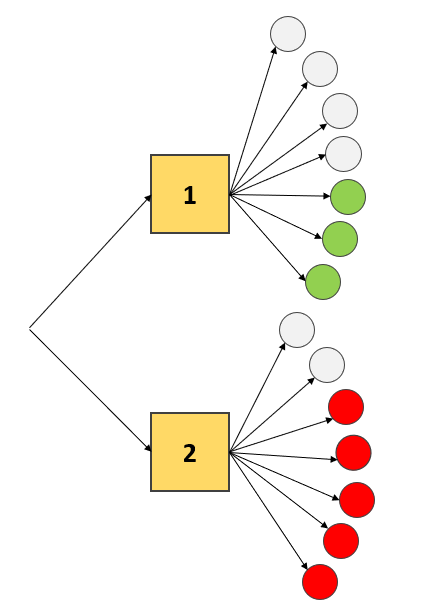
Ya que en ambas cajas hay bolas blancas, ambas contribuyen con su propia probabilidad al suceso de obtener una bola blanca durante la selección. Por esta razón, debemos aplicar la regla de la probabilidad total.
P\left(B\right)=P\left(1\right)P\left(B/1 \right)+P\left(2\right)P(B/2)
Seleccionar una u otra caja tiene una probabilidad del 0.5.
P\left(1\right)=P\left(2\right)=0.5
Por otra parte, la probabilidad de sacar una bola blanca en cada caja es:
P\left(B/1\right)=4/7
P\left(B/2\right)=2/7
Sustituimos.
P\left(B\right)=\left(0.5\right)\left(\frac{4}{7}\right)+\left(0.5\right)\left(\frac{2}{7}\right)=\frac{3}{7}
La probabilidad de extraer una bola blanca de las cajas es del 42.86%.
Comparando con las opciones, la respuesta correcta es la a).
Reactivo 46
Juan está diseñando un juego de azar para colocar un puesto en la feria de la ciudad el fin de semana. Él es buen vendedor y también matemático desde chico y sabe que tiene que maximizar su ganancia sin estafar a sus clientes.
El juego que ha pensado Juan dice así:
En una caja hay 4 tarjetas blancas y 6 tarjetas rojas. El jugador debe extraer una primera vez y agregar 3 tarjetas del color que le ha salido junto a la tarjeta que ha sacado, luego extrae una segunda vez y se queda con dicha carta. El jugador gana si la segunda vez logra extraer una tarjeta blanca.
Las reglas de la feria establecen que la probabilidad de ganar no debe ser menor al 35% si no, se considera una estafa. ¿Juan cumple las reglas con su juego?
- No cumple
- Si cumple
- Está en el límite
Solución:
Haciendo a un lado el extenuante enunciado, lo que tenemos es un experimento aleatorio que consiste de una caja con 6 tarjetas rojas y 4 blancas. En la primera extracción según el color se devuelve a la caja y se agregan 3 cartas del mismo color, esto hace que el total de cartas suba de 10 a 13.
Distinguimos entonces entre dos sucesos incompatibles seleccionar la primera vez rojo y seleccionar la segunda blanca. Debemos aplicar la propiedad de probabilidad total.
\mathrm{R}=extraer rojo la primera vez
\mathrm{B}=extraer blanco la primera vez
P\left(B\right)=P\left(R\right)P\left(R/B\right)+P\left(B\right)P\left(B/B\right)
La probabilidad de extraer rojo o blanco a la primera se calcula como:
P\left(R\right)=\frac{6}{10}
P\left(B\right)=\frac{4}{10}
La probabilidad de extraer blanco la segunda vez, habiendo sacado rojo la primera es:
P\left(R/B\right)=\frac{4}{13}
La probabilidad de extraer blanco la segunda vez, habiendo sacado blanco la primera es:
P\left(B/B\right)=\frac{7}{13}
Sustituyendo:
P\left(B\right)=\frac{6}{10}\frac{4}{13}+\frac{4}{10}\frac{7}{13}=\frac{52}{130}=0.4
La probabilidad de que sus clientes ganen es del 40%, Juan cumple con el reglamento de la feria.
Seleccionamos como respuesta correcta la b).
Reactivo 47
Dos fábricas deciden hacer un convenio para suplir una misma materia prima en la capital de México. A la Empresa A le ha tocado suplir el 45% de la producción y a la empresa B el resto. Si la empresa A tiene un porcentaje del 10% de productos defectuosos y B un 8%.
¿Cuál es la probabilidad de que un usuario adquiera un producto defectuoso?
- 8.9\%
- 10\%
- 9\%
Solución:
En este caso, entendemos que el producto puede venir de la empresa A o de la empresa B y cada una de ellas posee un porcentaje distinto de sacar al mercado un producto defectuoso, por tanto, debemos aplicar el teorema de la probabilidad total.
P\left(ME\right)=P\left(A\right)P\left(ME/A\right)+P\left(B\right)P\left(ME/B\right)
Donde:
- P\left(A\right) es la probabilidad de escoger a la empresa A
- P\left(B\right) es la probabilidad de escoger a la empresa B
- ME producto en mal estado
El enunciado nos da la siguiente información:
- P\left(A\right)=0.45
- P\left(B\right)=0.55
- P\left(ME/A\right)=0.1
- P\left(ME/B\right)=0.08
Sustituimos.
P\left(ME\right)=\left(0.45\right)\left(0.1\right)+\left(0.55\right)\left(0.08\right)=0.089
La probabilidad de que un usuario compre un producto en mal estado es del 8.9%.
Comparando con las opciones, seleccionamos como respuesta correcta la a).
Reactivo 48
Si se quiere representar la probabilidad del experimento de lanzar una moneda y luego un dado o una moneda, en función del primer resultado mediante algún tipo de distribución, ¿de qué tipo sería?
- Continua
- Discreta
- Discontinua
Solución:
Recordemos que las distribuciones de probabilidad son funciones matemáticas que permiten asignar a cada suceso de un experimento aleatorio una probabilidad a la ocurrencia de dicho suceso.
Ahora, existen variables que pueden tomar cualquier valor (continuas) y otras que solo pueden tomar ciertos valores de un conjunto finito (discretas), por esta razón, existen distribuciones de probabilidad para variables continuas y variables discretas.
El caso planteado en el enunciado corresponde a un experimento con variable discreta, por esta razón, el tipo de distribución a escoger es de tipo discreta. Concluimos seleccionando como correcta la opción b).
Reactivo 49
A las funciones que asignan una probabilidad a un suceso específico de un experimento aleatorio se denominan:
- Teorema de la suma
- Probabilidad total
- Distribución de probabilidad
Solución:
En probabilidad clásica, la magnitud que nos permite cuantificar la posibilidad de ocurrencia para un suceso dado, se calcula como el cociente entre los eventos favorables sobre los eventos totales del experimento.
Este concepto puede extenderse entendiendo que, matemáticamente, las funciones son herramientas que permiten asignar un resultado único a cada valor de una variable. Pero, en realidad, no todos los experimentos aleatorios tienen las mismas probabilidades o se comportan de la misma forma.
Por esta razón, es necesario incluir el concepto de distribución de probabilidad como funciones matemáticas que permiten establecer un modelo de comportamiento para algunos sistemas reales.
Concluimos entonces que la respuesta correcta es la c).
Reactivo 50
Relacione la distribución de probabilidad con el tipo de variable aleatoria a la que pertenece.
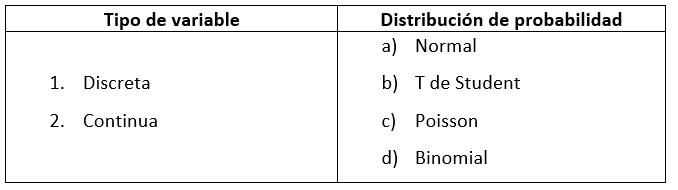
- 1cd y 2ab
- 1ab y 2cd
- 1ac y 2bd
Solución:
Debido a que las funciones de probabilidad permiten describir el comportamiento de una variable aleatoria según el modelo al que pertenezca, es necesario realizar funciones que se adapten a variables discretas y otras a variables continuas.
No es igual estudiar la probabilidad del experimento de un dado, en el que solo hay 6 posibles resultados, que la estatura de los recién nacidos en una sala de maternidad. Una variable es discreta y la otra es continua.
A partir de la teoría referente a distribuciones de probabilidad, las más empleadas en cada caso son:
Variables discretas.
- Hipergeométrica
- Poisson
- Binomial
Variables continuas.
- Normal o Gaussiana
- De Pareto
- T de Student
En base a esto, realizamos el pareo correspondiente a las columnas de la tabla: 1cd y 2ab.
Comparando con las opciones, seleccionamos como correcta la a).


