Resolvemos la Guía Interactiva de EXANI II de Matemáticas Financiera. En esta ocasión, vamos con la primera parte desde el ejercicio 1 hasta el 12.

Matemáticas financieras es una asignatura sustentada en conceptos de economía y finanzas que debes manejar. Antes de resolver los reactivos, consulta la bibliografía recomendada por el EXANI-II.
Estructura del EXANI II
La prueba de admisión diseñada por Ceneval, está compuesta por dos grandes áreas, ambas con la misma importancia en la nota final:
- Habilidades y conocimientos
- Los módulos específicos.
También existe una prueba diagnóstico de inglés aplicada por algunas universidades y cuyo resultado no se toma en cuenta para la nota.
Examen de habilidades y conocimientos
Esta primera parte es igual para todas las carreras y se compone por: 60 ejercicios de Español y 30 de Matemáticas. La siguiente tabla resume la distribución de los reactivos en la prueba de ingreso EXANI II:
Estructura del examen y la guía del EXANI II
| Área | Reactivos |
|---|---|
| Habilidades y conocimientos | |
| Pensamiento matemático | 30 |
| Comprensión lectora | 30 |
| Redacción indirecta | 30 |
| Módulos de conocimientos específicos | |
| Módulo 1 | 24 |
| Módulo 2 | 24 |
| Subtotal de reactivos | 138 |
| Diagnóstico | |
| Inglés | 30 |
| Total de reactivos | 168 |
Conocimientos específicos
En la segunda parte pueden salir 2 de 15 módulos, los cuales varían de acuerdo con la carrera. Es necesario que revises la convocatoria de tu universidad para conocer qué módulos debes estudiar.
Módulos de los conocimientos específicos
| 1. Administración | 9. Física |
| 2. Aritmética | 10. Historia |
| 3. Biología | 11. Literatura |
| 4. Cálculo diferencial e integral | 12. Matemáticas financieras |
| 5. Ciencias de la Salud | 13. Premedicina |
| 6. Derecho | 14. Probabilidad y estadística |
| 7. Economía | 15. Química |
| 8. Filosofía | 16. Psicología |
Temario Matemáticas financieras EXANI II
A continuación te dejo la distribución de los 24 reactivos de matemáticas financieras, junto a los temas que van para el examen.
| Subárea | Reactivos |
|---|---|
| Elementos financieros básicos | 14 |
| Interés simple | 10 |
| Total | 24 |
Subárea: Elementos financieros básicos
- Razón aritmética a partir de su antecedente y consecuente y como proporción
- Proporcionalidad directa e inversa en el ámbito financiero
- Cantidad inicial y final, incremento y decremento
- Precio inicial, porcentaje de descuento y precio final
- Términos, diferencias y valores faltantes de sucesiones con números enteros y fraccionarios
Subárea: Interés simple
- Saldo insoluto
- Tasa y periodo de interés
- Monto de inversión
- Tiempo de inversión
- Capital de inversión
Recomendaciones para resolver la guía interactiva
Te dejo algunos trucos para sacarle el máximo provecho a la guía EXANI II 2023 que puedes tener en cuenta a la hora de estudiar:
- Elimina las distracciones. Ve a un sitio en el que te sientas cómodo o cómoda, coloca tu teléfono en modo avión y mantén cerca de ti lapiceros, borrador y libretas.
- No te enfoques en el resultado, sino en el procedimiento. Coloca toda tu atención en analizar y desglosar los problemas para identificar las herramientas que debes usar. Una buena estrategia conlleva a buenos resultados.
- Lleva el tiempo mientras resuelves la guía. Mide el tiempo durante cada sesión de estudios, buscando acortar el tiempo lo más que puedas antes del examen.
- Si un reactivo parece demasiado difícil, ve al siguiente. Evita caer en frustración mientras estudias, mantener el foco y meditar esos ejercicios difíciles, te permitirán desarrollar capacidades analíticas sólidas.
Reactivo 1
Determine a cuánto asciende la deuda de una persona si el banco le prestó \frac{2}{3} de $ 900,000, y ahora es \frac{6}{8} menor que hace 5 meses.
- $ 150,000
- $ 450,000
- $ 1,050,000
Solución:
Primero debemos calcular la deuda inicial, multiplicando \frac{2}{3} por $ 900,000.
{\mathrm{R}}_{1}=\left(\frac{2}{3}\right)\left(\mathrm{900,000}\right)=\$\mathrm{600,000}
La deuda inicial es de 600,000 pesos. Ahora, se toma el valor anterior y se multiplica por \frac{6}{8} para obtener la deuda 5 meses después.
{\mathrm{R}}_{2}=\left(\frac{6}{8}\right)\left(\mathrm{600,000}\right)=\$\mathrm{450,000}
Restamos las cantidades anteriores para obtener la respuesta correcta.
d=\mathrm{600,000}-\mathrm{450,000}=\$\mathrm{150,000}
La respuesta correcta es el inciso a). El error en el inciso b) es que no se ha calculado la resta entre los dos montos del préstamo, se ha llegado hasta 450,000. Por otra parte, el error de la opción c) es que en lugar de restar las deudas se suman, dando como resultado $ 1,050,000.
Reactivo 2
Para producir 3.5 toneladas de tela se paga un total de $ 2,450. Si se necesita producir 8 toneladas, ¿cuál es la proporción de la variación que representa los datos proporcionados?
- 3.5 es a 8 como $ 5,600 a $ 2,450
- 3.5 es a $ 2,450 como 8 es a $ 5,600
- 3.5 es a $ 5,600 como 8 es a $ 2,450
Solución:
Primero se aplica una regla de tres directa para obtener el precio a pagar.
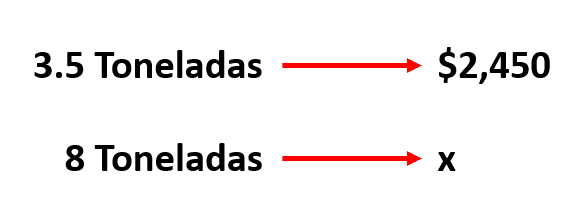
x=\frac{\left(8\right)\left(2450\right)}{3.5}=\$\mathrm{5,600}
Por lo tanto, la proporción correcta es: 3.5 es a $ 2,450 como 8 es a $ 5,600.
La respuesta correcta es el inciso b). Tanto en el inciso a) como en el c), se sustituye de forma errónea los valores en la proporción.
Reactivo 3
Si una persona tiene en el banco un saldo de $ 400, de los cuales una parte son ahorros y los otros intereses en una razón de 3:2, ¿cuál es la proporción representada?
- \frac{3}{2}=\frac{240}{160}
- \frac{3}{2}=\frac{160}{240}
- \frac{2}{3}=\frac{240}{160}
Solución:
Iniciamos identificando que la proporción 3:2 es equivalente a 3/2 . Por otra parte, la suma de los ahorros con los intereses debe ser igual a $ 400.
400=a+i
Mientras que la proporción es igual al cociente de los ahorros y los intereses \frac{3}{2}=\frac{a}{i} , porque los intereses son una fracción del monto base y, por ende, i no puede ser mayor que a . Con esto nos queda:
\left\{\begin{array}{c}a+i=400\\ a=\frac{3}{2}i\end{array}\right.
Con este sencillo sistema de ecuaciones encontramos el valor de los ahorros y los intereses. Sustituyendo la proporción en la primera ecuación se obtiene:
\frac{3}{2}i+i=400\to \frac{5}{2}i=400
\therefore i=\$160
Los ahorros se obtienen restando 160 a los 400.
a=400-160=240
Finalmente:
\frac{3}{2}=\frac{240}{160}
La respuesta correcta es el inciso a). Tanto en el inciso b) como en el c), se utiliza de forma incorrecta la proporción. En la primera se escribe al revés el ahorro y los intereses, mientras que en la segunda el \frac{3}{2} .
Reactivo 4
¿Qué porcentaje representa el aumento en el precio por litro de gasolina que, al iniciar el año era de $ 14 y el incremento que se realizó es de $ 3?
- 0.42%
- 14.17%
- 21.43%
Solución:
El incremento se calcula respecto al precio inicial aplicando la siguiente fórmula:
{\mathrm{\Delta }}_{\%}=\frac{\mathrm{\Delta }P}{{P}_{1}}\cdot 100\%
Donde \mathrm{\Delta }P es la variación del precio y {P}_{1} es el precio inicial. Sustituyendo se obtiene:
{\mathrm{\Delta }}_{\%}=\frac{3}{14}\cdot 100\%=21.43\%
El incremento en el precio de la gasolina fue del 21.43%.
La respuesta correcta es el inciso c). El error de la opción a) ocurre al multiplicar el incremento con el precio original. Por otra parte, en el inciso b) se lleva a cabo un procedimiento distinto. Se suma el precio con el incremento, luego se divide entre 100 y luego se suma a los $ 14.
Reactivo 5
Una línea aérea oferta 320 lugares a un costo de $ 5,400 para obtener sus gastos. Si sólo vende 180 lugares, ¿a qué costo deberá tener el pasaje para cubrir los gastos?
- $ 3,037.50
- $ 8,437.50
- $ 9,600.00
Solución:
Primero obtenemos el total de gastos de la aerolínea multiplicando los puestos por el precio inicial.
S=\left(320\right)\left(5400\right)=\$\mathrm{1,728,000}
Este es el monto que deben cubrir los 180 asientos vendidos. El precio se obtiene dividiendo el monto anterior por los asientos vendidos.
R=\frac{1728000}{180}=\$\mathrm{9,600}
Si solo se venden 180 asientos, estos se deben vender en $ 9,600 para cubrir gastos.
La respuesta correcta es el inciso c). El resultado del inciso a) es incorrecto porque los gastos del viaje son iguales, pero disminuye la cantidad de lugares vendidos, por lógica el nuevo precio debe ser mayor. Acá se multiplica 180 por 5400 y se divide entre el total de asientos.
Por otra parte, en el inciso b) se calcula el porcentaje de los lugares vendidos y que se multiplica por el costo de los lugares ofertados inicialmente
Reactivo 6
Determine la tasa de interés de una inversión que se colocó durante 1 mes con un capital inicial de $ 10,000 y un saldo final de $ 10,500.
- 05%
- 00%
- 24%
Solución:
Los intereses relacionados con una inversión, son el beneficio monetario obtenido por el desarrollo de un proyecto financiero y representa un porcentaje del valor inicial abonado.
En este caso, la inversión inicial fue de $ 10,000 y el retorno final de $ 10,500. Esto quiere decir que se han obtenido $ 500 por concepto de intereses.
I=\$500
La tasa de interés (porcentaje) se obtiene dividiendo los intereses (unidades monetarias) por el monto inicial.
i=\frac{500}{10000}\cdot 100\%=5\%
El proyecto de inversión tiene una tasa de interés del 5% mensual.
La respuesta correcta es el inciso b). Otra forma de obtener este resultado, sería aplicando la fórmula de interés simple:
S=P\left(1+ni\right)
Donde n es el total de períodos, i es la tasa de interés y P es el monto inicial. El error en el inciso a) es que se dividen los $ 10,500 entre los $ 10,000 y el resultado se toma como porcentaje.
Por otro lado, en el inciso c) se dividen los $ 10,000 sobre el retorno de $ 10,500 y luego se multiplica por 100%.
Añadido:
Reactivo 7
Calcule el precio total que se debe pagar por la compra de dos casas de campaña, cuyo precio de lista es de $ 55,499.00 cada una, considerando que hay una oferta que indica que al llevar dos, la segunda tiene una rebaja de 15%.
- $ 94,348.30
- $ 102,673.15
- $ 119,322.85
Solución:
Debido a que el descuento se aplica a la segunda casa, la primera se paga a precio completo. El pago final se calcula como:
R={S}_{1}+{S}_{2}\left(1-D\right)
Donde {S}_{1} y {S}_{2} es el precio de la casa de campaña y D es el descuento expresado en decimales. Sustituyendo los valores nos queda:
R=55499+55499\left(1-0.15\right)=\$102673.15
El total a pagar por las dos casas de campaña es de $ 102,673.15.
La respuesta correcta es el inciso b). El error en el inciso a) consta en aplicar el descuento a la suma del precio de las dos casas, de esta forma, se obtiene que: \left(55499+55499\right)\left(1-0.15\right)=94348.3 .
Por otra parte, en el inciso c) en lugar de descontar el 15% a la segunda casa, se adiciona este porcentaje al precio de la casa, pagando $ 63,823.85 por la segunda y $ 55,499 por la primera. Sumando ambos montos, se obtiene: $ 119,322.85.
Reactivo 8
¿Cuánto es el saldo insoluto por pagar a los 3 meses sobre una deuda adquirida al comprar un equipo de cómputo de $ 46,200, con una facilidad de pago de 5 mensualidades y una tasa de 5% al mes?
- $ 9,240
- $ 18,480
- $ 27,720
Solución:
El saldo insoluto, es el dinero que falta por pagar luego de pagar las cuotas de los 3 primeros meses. Este préstamo se paga en cuotas de interés simple y que amortizan la misma cantidad de capital inicial en cada una de ellas.
Esto quiere decir que la amortización es constante durante los 8 meses.
A=\frac{46200}{5}=\$\mathrm{9,240}
En cada mes, se pagan 9,240 pesos del capital inicial. Al encontrarnos en el tercer mes, aún quedan los períodos desde el mes 4 hasta el 5, es decir, quedan 2 mensualidades. Por lo tanto, el monto insoluto se calcula como:
\mathrm{P}\mathrm{I}=2\left(9240\right)=\$\mathrm{18,480}
La respuesta correcta es el inciso b). En el inciso a) se calcula el monto insoluto para el mes 4, es decir, solo queda por amortizar el mes 5 y esto da un total de 9240 pesos. Por otro lado, en el inciso c) se calcula el monto amortizado, no el monto por amortizar:
\frac{46200}{5}\cdot 3=\$\mathrm{27,720}
Reactivo 9
¿Cuál era el costo original de un televisor, si su precio de mostrador es de $ 15,800 y ya incluye un descuento de 15%?
- $ 18,170.00
- $ 18,588.23
- $ 23,700.00
Solución:
Para aplicar un descuento a un producto, se aplica la siguiente fórmula:
S=P\left(1-D\right)
Donde S es el precio final, P el precio original y D es el descuento. El enunciado indica el precio después del descuento y el porcentaje de descuento, despejamos el precio inicial de la ecuación.
P=\frac{S}{1-D}
Sustituimos.
P=\frac{15800}{1-0.15}=18588.23
El precio original del televisor era de $ 18,588.23
La respuesta correcta es el inciso b). En el inciso a) se comete un error al sumar el descuento aplicado sobre los $ 15,800 es decir 15800\cdot 0.15=2370 y este resultado se suma a los $ 15,800 obteniendo $ 18,700.
La opción c) muestra el resultado de aplicar de forma incorrecta el porcentaje del 15% al precio final: 15800\cdot 1.5=23700 .
Reactivo 10
Encuentre el cuarto término de la sucesión aritmética.
\frac{15}{8},\frac{7}{4},\frac{13}{8}, \dots
- \frac{5}{4}
- \frac{3}{2}
- \frac{11}{8}
Solución:
Las series aritméticas tienen como propiedad, que la diferencia entre términos consecutivos es constante.
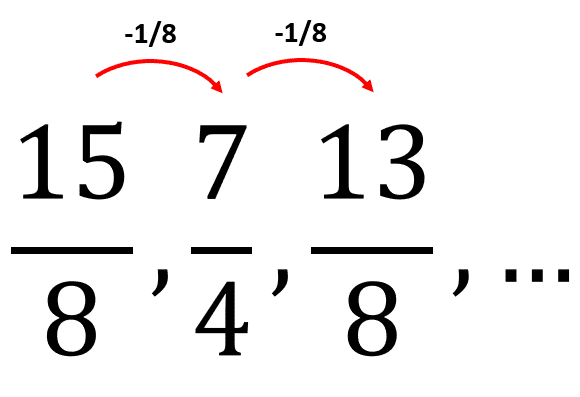
Si el cuarto término es el que continúa la serie, le restamos \frac{1}{8} a \frac{13}{8} para obtener el cuarto elemento.
{a}_{4}=\frac{13}{8}-\frac{1}{8}=\frac{3}{2}
Finalmente:
\frac{15}{8},\frac{7}{4},\frac{13}{8},\frac{3}{2},\dots
La respuesta correcta es el inciso b). En el inciso a) se comete un error al tomar como siguiente término la diferencia de 2 unidades en el numerador respecto a la fracción de \frac{7}{4} . Por otro lado, el inciso c) muestra como resultado al quinto elemento de la serie, no al cuarto.
Reactivo 11
Es la ganancia por invertir dinero, es decir, la cantidad que se pagará por este.
- Monto
- Interés
- Capital
Solución:
Respecto a una inversión, el dinero extra que recibe el inversionista respecto a la inversión inicial se denomina interés y corresponde a la ganancia por el uso de su capital inicial para llevar a cabo un proyecto financiero.
La respuesta correcta es el inciso b). El monto es una cantidad de dinero que se recibirá en el futuro como la suma del capital más los intereses. Mientras que el capital es la cantidad de dinero invertida al inicio del proyecto.
Reactivo 12
¿A qué tasa de interés anual un capital de $ 65,000 invertido en una cuenta bancaria produce un monto de $ 85,000 en 4 años?
- 5.23%
- 7.69%
- 30.77%
Solución:
Para resolver el problema, recurrimos a la fórmula de interés simple.
S=P\left(1+ni\right)
Donde S es el dinero al final de n periodos, P es el capital inicial e i es la tasa de interés. Despejamos la tasa de interés de la ecuación.
1+ni=\frac{S}{P}\to ni=\frac{S}{P}-1
i=\frac{1}{n}\left(\frac{S}{P}-1\right)
Sustituimos.
i=\frac{1}{4}\left(\frac{85000}{65000}-1\right)=0.0769
La tasa de interés es del 7.69%.
La respuesta correcta se encuentra en el inciso b). En la opción a) se comete un error conceptual en el cálculo, pues se dividen los $ 85000 entre el capital inicial y el resultado se multiplica por los 4 años.
Por otra parte, en el inciso a) se omite la división entre el número de años: i=\left(\frac{85000}{65000}-1\right) .

