Solución de la segunda y última parte de la guía interactiva del EXANI II 2023 resuelta, correspondiente a Matemáticas Financieras desde el reactivo 13 hasta el 24.

Recuerda que puedes continuar estudiando el resto de módulos con los materiales EXANI II, para convertirte en un aspirante seleccionado.
Reactivo 13
Si una persona desea obtener al finalizar 1 año el monto de $10,000.00, ¿qué cantidad debe depositar hoy en un banco que ofrece una tasa de interés simple de 12% anual?
- $8,928.57
- $10,833.33
- $11,200.00
Solución:
Es necesario utilizar la fórmula de interés simple.
S=P\left(1+ni\right)
Se requiere conocer cuál debe ser el monto inicial para obtener 10000 pesos luego de 1 período con una tasa de interés del 12%. Despejamos a P .
P=\frac{S}{1+ni}
Evaluamos la expresión.
P=\frac{10000}{1+\left(1\right)\left(0.12\right)}=8928.57
Se deben depositar $8,928.57 para obtener al cabo de un año $10,000 a una tasa de interés simple del 12%. La respuesta correcta es el inciso a).
En la opción b) se toma el monto, se divide por 12 y el resultado se suma con los 10,000 pesos. Por otra parte, en el inciso c) se consideran los 10,000 pesos como capital y no como retorno.
Reactivo 14
Calcule el monto actual de la inversión de una persona si al inicio tenía $218,000 y ha utilizado 2/5 de la misma.
- $87,200
- $130,800
- $305,200
Solución:
Para calcular cuánto le queda a la persona luego de gastar 2/5 del monto inicial, se le restan a los $218,000 pesos el producto \left(\frac{2}{5}\right)\left(218000\right) .
S=218000-\left(\frac{2}{5}\right)\left(218000\right)=130800
Al usuario le quedan $130,800.
Respuesta correcta: b). En el inciso a) se multiplica el 2/5 por el capital inicial, pero no se resta el resultado al monto inicial. Acá se obtiene cuánto se gastó, no cuánto ha quedado. La opción c) en lugar de restar los 87,200$ que se gastaron, los suma con el monto inicial.
Reactivo 15
Una persona solicita un préstamo por $60,000 a un plazo de 12 meses. Si en el primer mes paga $8,000 de su deuda y en el doceavo $5,250, ¿cuál es la diferencia entre los pagos que efectúa mensualmente?
- -$250
- -$229
- $250
Solución:
En este caso podemos ver a los pagos como una serie aritmética, los cuales disminuyen con una diferencia d constante que debemos calcular. La fórmula para una serie aritmética es:
{a}_{n}={a}_{1}+d\left(n-1\right)
Despejamos la diferencia.
d=\frac{{a}_{n}-{a}_{1}}{n-1}
Tenemos la cuota del primer mes y del último: {a}_{12}=5250 , n=12 , sustituyendo nos queda:
d=\frac{5250-8000}{12-1}=-250\$
La diferencia entre los pagos de la deuda fue de -250 pesos.
La respuesta correcta es el inciso a). El error en el inciso b) es que la diferencia entre la última y la primera cuota se divide entre 12 y no 11 meses. Por otro lado, en la opción c) la resta entre las cuotas se hace al revés, primera menos última en lugar de última menos primera.
Reactivo 16
Obtenga el monto de la rebaja en la compra de 1 computadora con precio inicial de $38,000.00 y que se ofrece en tienda con un 15%.
- $2,533.33
- $5,700.00
- $32,300.00
Solución:
Para el monto de la rebaja, se multiplica el costo inicial de la computadora por el descuento
{P}^{\text{'}}=P\cdot D
Sustituimos el precio inicial P=38000 y el descuento en decimales D=0.15 .
{P}^{\text{'}}=38000\cdot 0.15=5700\$
La respuesta correcta es el inciso b). En la opción a) se divide el monto inicial por 15, procedimiento que es totalmente incorrecto y en la opción c) se calcula el nuevo monto a pagar, no el monto del descuento.
Reactivo 17
¿Cuál es el precio final de una vacuna cuyos insumos de producción equivalen a $1,213.00 y el laboratorio proyecta una ganancia de 25%?
- $1,238.00
- $1,261.52
- $1,516.25
Solución:
La ganancia se calcula sumando al costo de producción, el producto del porcentaje por el costo.
P=1213+1213\cdot 0.25=1516.25\$
La vacuna debe venderse a 1,516.25 pesos para obtener una ganancia del 25%.
Respuesta correcta: c). En el inciso a) se le ha sumado 25 al costo de producción, mientras que en el inciso b) se realiza el siguiente procedimiento: \left(\frac{1213}{25}\right)+1213 . Ambos métodos de cálculo son incorrectos.
Reactivo 18
¿Qué porcentaje de descuento se le aplica al sueldo de una persona que percibe $11,460, al cual se le cobra un préstamo personal, y recibe al final únicamente $10,300?
- 10.12%
- 11.26%
- 11.60%
Solución:
Los descuentos se calculan como:
{P}^{\text{'}}=P\left(1-D\right)
Donde D es el porcentaje a descontar. Despejamos a D de la ecuación y evaluamos.
D=1-\frac{{P}^{\text{'}}}{P}=1-\frac{10300}{11460}
D=0.1012
Al empleado se le descontó un 10.12% de su salario por concepto de préstamo.
La respuesta correcta es el inciso a).
Si has seleccionado la opción b) probablemente hayas calculado la diferencia de los sueldos y el resultado se multiplica por 100. Por otro lado, en la opción c) la diferencia entre los sueldos se divide por 100. Ambos procedimientos son erróneos.
Reactivo 19
¿Cuánto debe pagar una persona por concepto de intereses de una deuda por $50,000, si la liquida 2.5 años después, a una razón de 25% anual?
- $12,500
- $20,000
- $31,250
Solución:
Los intereses simples se calculan como el producto del monto inicial, por la tasa de interés, por los períodos transcurridos.
I=P\cdot n\cdot i
Sustituimos los valores, todos suministrados por el enunciado.
I=\left(50000\right)\left(2.5\right)\left(0.25\right)=31250\$
El usuario debe pagar 31,230$ por concepto de intereses durante los 2 años y medio transcurridos.
La respuesta correcta es el inciso c). En la opción a) se multiplica el monto de la deuda por la tasa de interés, pero no se consideran los períodos. Mientras que, en el inciso b) se dividen los $50,000 entre 2.5, procedimiento totalmente erróneo.
Reactivo 20
Una empresa mayorista de papelería vende lápices con un precio inicial de $4.00. Por cada pieza extra disminuye 30 centavos, con un tope de compra de hasta 10 lápices. ¿Cuál es el precio que se paga por la octava pieza?
- $1.30
- $1.60
- $1.90
Solución:
A partir de la condición de rebaja indicada en el enunciado, la empresa calcula el cobro de pieza extra como:
S=4-0.3\left(n-1\right)
Por cada lápiz extra se restan 0.3 pesos (equivalente a 30 centavos), sin contar el primer lápiz, por esta razón se multiplica 0.3 por n-1 y no por n . Donde n representa la cantidad de lápices y la fórmula aplica hasta n\le 10 unidades. Sustituyendo n=8 nos queda:
S=4-0.3\left(8-1\right)=1.9\$
Si se compran 8 lápices, el octavo queda en 1.9 pesos.
La respuesta correcta es el inciso c). En el inciso a) se utiliza la fórmula correcta para el cálculo, pero en lugar de sustituir 8 se sustituyen 10 unidades. Por otro lado, en el inciso b) no se le resta 1 a los 8 lápices, es equivalente a usar 4-0.3n en lugar de 4-0.3\left(n-1\right) .
Reactivo 21
Si una persona desea invertir $40,000.00 en una cuenta de ahorros que ofrece una tasa de interés simple de 55% anual, ¿cuánto obtendrá al final en un plazo de 4 años?
- $62,000.00
- $128,000.00
- $230,880.25
Solución:
Se utiliza la fórmula de interés simple.
S=P\left(1+ni\right)
Donde S es el monto final, P es la inversión inicial, n es el número de períodos e i la tasa de interés. Sustituimos los datos:
S=\left(40000\right)\left(1+4\cdot 0.55\right)=\mathrm{128,000}\$
El usuario obtendrá un retorno de 128,000 pesos al cabo de 4 años.
La respuesta correcta es el inciso b). En el inciso a) se suman los intereses generados por el primer año 40000\left(1+0.55\right) , mientras que en el c) se ha utilizado la fórmula de interés compuesto: 40000{\left(1+0.55\right)}^{4}=\mathrm{230,880.25}\$ .
Reactivo 22
¿En cuánto tiempo un capital de $18,000 se convierte en $75,000, si la tasa de interés simple que ofrece una institución bancaria es de 41% anual?
- 1.70 años
- 4.16 años
- 7.72 años
Solución:
Para encontrar el total de períodos, empleamos la fórmula de interés simple:
S=P\left(1+ni\right)
Despejamos a n .
S=P\left(1+ni\right)\to n=\frac{1}{i}\left(\frac{S}{P}-1\right)
Sustituyendo los valores nos queda:
n=\frac{1}{0.41}\left(\frac{75000}{18000}-1\right)=7.72
El capital debe permanecer por 7.72 años en la cuenta bancaria para obtener un retorno de 75,000$. La respuesta correcta se encuentra en el inciso c).
En la opción a) se realiza un procedimiento similar al del inciso c) pero se olvida restar por 1: \frac{1}{0.41}\left(\frac{75000}{18000}\right) . Por otro lado, en el inciso b) se calculan los períodos como el cociente entre el retorno y la inversión n=\frac{75000}{18000} . Ambos procedimientos son incorrectos.
Reactivo 23
¿Durante cuánto tiempo se ha invertido un capital de $3,500,000 que produjo intereses de $2,600,000 a una tasa anual de 4%?
- 34 años
- 97 años
- 57 años
Solución:
Los intereses simples de una inversión se calculan como:
I=P\cdot i\cdot n
Donde P es el monto inicial, I son los intereses generados durante el periodo, i es la tasa de interés y n los períodos del proyecto financiero. Despejamos a n y sustituimos los valores conocidos.
n=\frac{I}{iP}
Sustituyendo se obtiene:
n=\frac{2600000}{\left(0.04\right)\left(3500000\right)}=18.57 \mathrm{a}\mathrm{ñ}\mathrm{o}\mathrm{s}
El capital ha permanecido 18.57 años en el proyecto de inversión, de tal forma que ha generado $2,600,000 pesos por concepto de intereses. La respuesta correcta es el inciso c). El error del inciso a) ocurre al dividir el capital sobre los intereses, mientras que en la opción b) se multiplica por la tasa de interés sin convertirla en decimal.
Reactivo 24
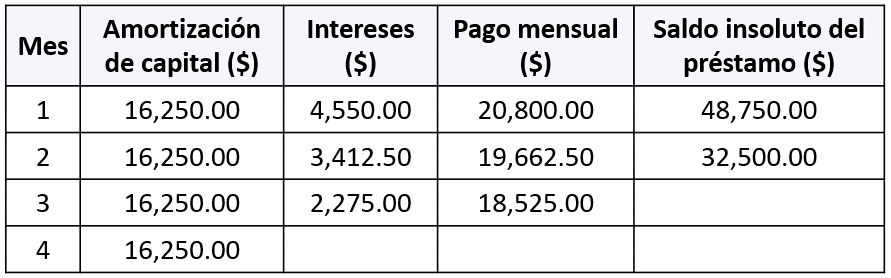
Se compra una televisión a crédito con precio de $65,000.00. El plazo establecido para el pago es de 4 meses con una tasa mensual de 7% y montos de amortización fija por $16,250.00. Considerando la tabla, ¿cuál es el saldo insoluto del préstamo para el tercer mes?
- $13,975.00
- $16,250.00
- $18,525.00
Solución:
El monto insoluto del préstamo en determinado mes o año, es el dinero que queda por pagar para el resto de períodos. En el esquema de amortización de este préstamo, todas las cuotas pagan la misma cantidad del capital inicial, tal como indica el enunciado.
Por esta razón, para el tercer mes el saldo insoluto es el correspondiente al mes cuatro, porque allí terminan los períodos del préstamo.
{\mathrm{S}\mathrm{I}}_{3}=\mathrm{16,250.00}\$
La respuesta correcta es la del inciso b). En el inciso a) se calcula la diferencia entre la amortización de capital y los intereses para el tercer mes; esto es incorrecto.
Por otro lado, en la opción c) se indica el monto de la cuota a pagar el tercer mes, cosa que no tiene relación alguna con el monto insoluto.


