Si llegaste hasta aquí, vas bien. En esta parte entramos a uno de los temas que sí o sí aparecen en el examen de admisión y que, curiosamente, hacen tropezar incluso a aspirantes que “eran buenos en mate” en la prepa: las funciones trigonométricas.

Y no, el problema casi nunca es que no se sepan la fórmula… El problema es cómo, cuándo y desde dónde aplicarla.
¿Qué temas abarca este examen simulador?
En estos 10 reactivos vas a trabajar lo que más preguntan en la UNAM, el IPN y el EXANI II cuando entra trigonometría:
- Conversión entre grados y radianes.
- Razones trigonométricas en triángulos rectángulos.
- Uso del círculo trigonométrico.
- Aplicaciones reales (altura, sombra y situaciones tipo examen).
- Identidades trigonométricas y relación entre seno, coseno y tangente.
- Interpretación de desplazamientos de fase en funciones.
Mis recomendaciones
- No empieces calculando. Primero ubica: ¿estás en grados o en radianes? Muchísimos errores vienen solo de eso.
- Dibuja el triángulo, aunque venga en la imagen. Dibujarlo tú te obliga a pensar qué lado es cuál.
- No memorices seno, coseno y tangente como letras; memorízalos como relaciones entre lados.
- En el círculo trigonométrico, primero ubica el cuadrante y luego el valor. El signo importa más que el número.
- Si un resultado “se ve bonito” pero no cuadra con el contexto, algo está mal.
- Entrena el ojo antes que la cuenta. Estima si el resultado debería ser grande, pequeño, positivo o negativo antes de calcular.
- Clasifica tus errores. No basta con saber que fallaste: ¿fue por signo?, ¿por confundir seno con coseno?, ¿por convertir mal?
- Aprende a soltar el reactivo. Si uno se atora, sigue. Ganar tiempo es tan importante como saber resolver.
¿Para qué sirven los simulacros?
Muchos aspirantes no se quedan por falta de conocimientos, sino porque el examen les gana en el ritmo y en los detalles: pierden mucho tiempo en un solo reactivo o se atoran en temas específicos que nunca pudieron dominar.
En resumen, no les alcanza el tiempo y quieren que, el día del examen, ese tema que nunca entendieron les salga bien.
Los simulacros sirven para eso: detectar temas exactos, entrenar el tiempo y llegar al examen sabiendo qué resolver primero y qué dejar al final. Esa es la diferencia entre quien “sabe” y quien sí se queda.
Reactivo 1: Conversión de grados a radianes
¿A cuánto equivale 45^\circ en radianes?
Reactivo 2: Conversión de radianes a grados
¿A cuántos grados equivalen 11/18 \pi radianes?
Reactivo 3: Razones trigonométricas – Coseno
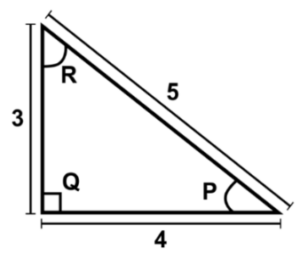
Usando los datos del siguiente triángulo rectángulo, el coseno del ángulo P es igual a:
Reactivo 4: Razones trigonométricas – Seno
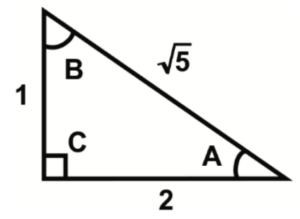
Determina el valor de \text{sen}(B) en el triángulo mostrado:
Reactivo 5: Aplicación de trigonometría – Altura y sombra
Un poste proyecta una sombra de 1.5 \text{ m} de longitud en el momento en el que el ángulo de elevación del sol es de 60^\circ . ¿Cuál es la altura del poste?
Considera lo siguiente: \text{sen } 60^\circ = 0.866, \cos 60^\circ = 0.5, \tan 60^\circ = 1.732
Reactivo 6: Triángulo rectángulo
En un triángulo rectángulo, la hipotenusa mide 10 unidades y uno de sus ángulos es de 30^\circ . ¿Cuántas unidades mide el lado opuesto al ángulo dado?
Reactivo 7: Coseno en el círculo trigonométrico
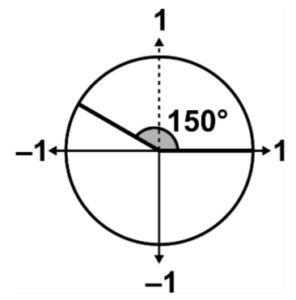
Calcula el valor del coseno para el ángulo de 150^\circ en el siguiente círculo trigonométrico:
Reactivo 8: Desplazamiento de fase
Selecciona la función que tiene un desplazamiento de fase de \pi unidades a la derecha:
Reactivo 9: Cociente de identidades trigonométricas
En términos de \text{sen } \theta y \cos \theta , \tan \theta es igual a:
Reactivo 10: Identidades pitagóricas
¿Qué expresión representa una de las llamadas identidades pitagóricas?


