Hola de nuevo aspirante. Si te estás preparando para el examen de admisión a la UNAM, al IPN o a cualquier universidad que aplique el EXANI II, este simulador también es para ti.
Esta es la segunda parte de los temas más preguntados en los exámenes de admisión. Después de productos notables y factorización, hay un bloque que siempre aparece: ecuaciones y funciones.
No importa la universidad, este tema nunca falla.
¿Qué vas a trabajar en este simulador?
En este simulador vas a resolver ejercicios de:
- Ecuaciones de primer grado
- Ecuaciones de segundo grado
- Sistemas de ecuaciones 2×2
- Funciones lineales
- Funciones cuadráticas
Todos los ejercicios están al mismo nivel de dificultad que encontrarás el día del examen.
¿Qué tipo de ejercicios vas a ver?
Vas a encontrar desde ecuaciones directas (incluyendo fracciones) hasta problemas donde tienes que plantear y no solo despejar. También vas a trabajar interpretación de funciones: leer una gráfica, reconocer pendiente, elegir la gráfica correcta y entender qué cambia cuando una función se desplaza.
- Ecuaciones lineales con despeje paso a paso
- Ecuaciones cuadráticas (diferencia de cuadrados y factorización)
- Sistemas 2×2 para encontrar valores exactos
- Modelos lineales a partir de una tabla
- Interpretación de gráficas de funciones lineales
- Parábolas: traslaciones, concavidad y relación entre ecuación y gráfica
¿Qué vas a aprender al resolverlos?
Vas a practicar cómo despejar variables paso a paso, entender qué representa cada número y leer una función tanto en forma numérica como en el plano cartesiano. Este tema suele generar muchos errores en el examen.
Cómo te recomiendo usar este simulador
Intenta resolver cada ejercicio por tu cuenta antes de ver la solución. Ahí es donde realmente detectas fallas y corriges procedimientos.
Las resoluciones completas las encontrarás en mi canal de YouTube, donde explico cada ejercicio paso a paso.
Reactivo 1: Ecuación lineal
¿Cuál es la solución de la ecuación 3x + 12 = 2 - x ?
Reactivo 2: Ecuación lineal
La solución de la ecuación 8x + 4 = 2x + 8 es:
Reactivo 3: Ecuación de primer grado y segmentos proporcionales
Observe los siguientes segmentos y sus longitudes, algunas expresadas en términos de x .
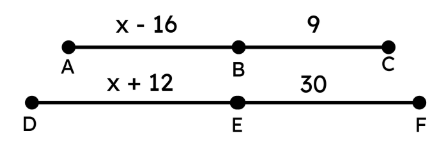
¿Para qué valor de x se cumple que \frac{\overline{AB}}{\overline{BC}} = \frac{\overline{DE}}{\overline{EF}} ?
Reactivo 4: Ecuación lineal con fracciones
El valor de x en la ecuación \frac{x}{3} + \frac{2}{5} = \frac{x}{2} - 1 es:
Reactivo 5: Ecuación lineal fraccionaria
El valor de “ x ” en la ecuación \frac{x - 2}{3} + \frac{x + 2}{5} = \frac{28}{15} es:
Reactivo 6: Diferencia de cuadrados
Las raíces de la ecuación x^2 - 64 = 0 son:
Reactivo 7: Diferencia de cuadrados
Las raíces de la ecuación 9x^2 - 49 = 0 son:
Reactivo 8: Ecuación de segundo grado
Una solución de la ecuación x^2 - 9x + 14 = 0 es:
Reactivo 9: Ecuación de segundo grado
Resuelve la ecuación x^2 - 7x = -12 .
Reactivo 10: Ecuación de segundo grado y segmentos proporcionales
Observe los siguientes segmentos y sus longitudes, algunas expresadas en términos de x .
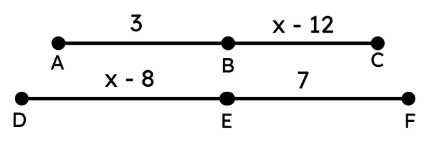
¿Para qué valor de x se cumple que \frac{\overline{AB}}{\overline{BC}} = \frac{\overline{DE}}{\overline{EF}} ?
Reactivo 11: Sistema de ecuaciones 2×2
¿Cuál es el valor de y al resolver el siguiente sistema de ecuaciones?
\begin{cases} x + y = 150 \\ 3x - y = 50 \end{cases}
Reactivo 12: Sistema de ecuaciones 2×2
¿Cuál es la solución del siguiente sistema de ecuaciones?
\begin{cases} 3x + y = 13 \\ 2x - 3y = -6 \end{cases}
Reactivo 13: Modelo lineal a partir de datos en tabla
Una compañía de transporte de carga pesada lleva un registro de los kilómetros recorridos y el costo total facturado en sus últimos viajes. Los datos se presentan en el siguiente cuadro:
| Kilómetros recorridos ( x ) | Costo del servicio ( y ) |
|---|---|
| 150 | $425 |
| 200 | $500 |
| 350 | $725 |
| 500 | $950 |
¿Qué modelo representa el costo del servicio de transporte, de acuerdo con el número de kilómetros recorridos?
Reactivo 14: Modelo de función lineal
Encuentra la gráfica de la función
f(x)=\frac{4}{3}x+4
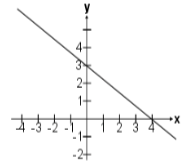
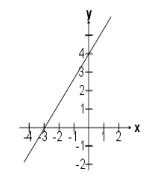
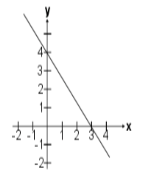
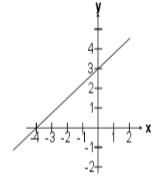
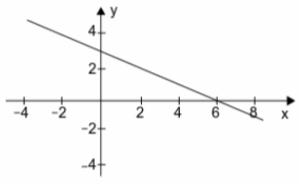
Reactivo 15: Gráfica de una función lineal
¿Cuál de las siguientes gráficas representa a la función f(x) = \frac{1}{2}x - 3 ?
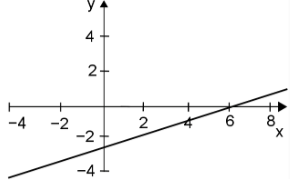
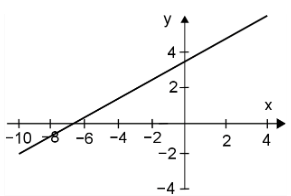
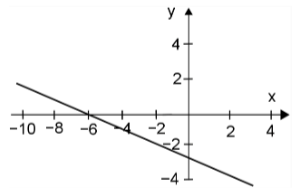
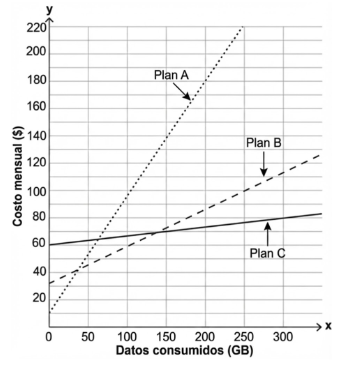
Reactivo 16: Análisis de pendiente
El siguiente gráfico muestra el costo mensual total ( y ) de tres planes de celular diferentes en función de la cantidad de gigabytes (GB) de datos consumidos ( x ). ¿Cuál de los planes cobra menos por cada Gigabyte (GB) adicional consumido?
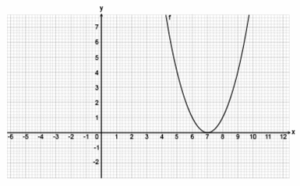
Reactivo 17: Gráfica de una parábola con traslación
¿Cuál es la gráfica que representa a la parábola y = (x - 8 - 1)^2 ?
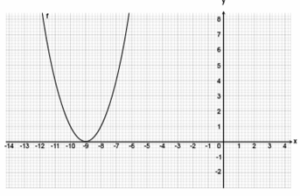
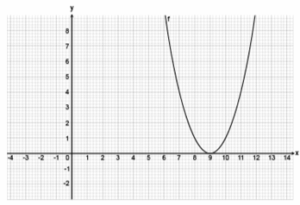
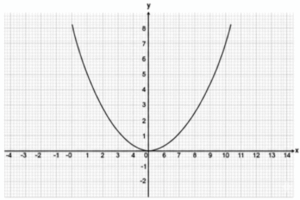
Reactivo 18: Traslación horizontal de una parábola
La gráfica describe la función y = -x^2 .
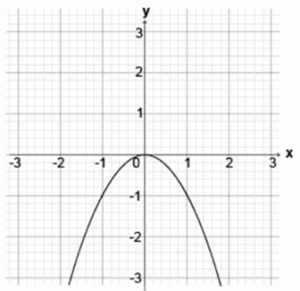
Se modifica la posición de la función y la expresión final es:
y = -(x + 4)^2
¿Qué transformación representa este diseño final respecto al diseño preliminar?
Reactivo 19: Relación entre ecuaciones cuadráticas y sus gráficas
Relacione las ecuaciones que reflejan cambios en los coeficientes con las gráficas que los representan:
Ecuación:
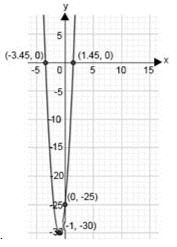
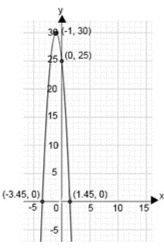
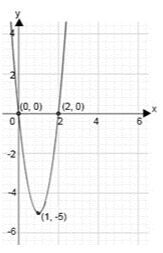
- y = 5x^2 - 10x
- y = -5x^2 - 10x + 25
- y = 5x^2 + 10x - 25
Gráfica:
Reactivo 20: Transformación y concavidad de la parábola
En el plano se observa la gráfica de la función:
f(x) = -ax^2 - 2ax - a
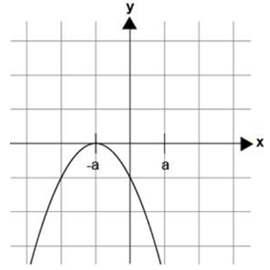
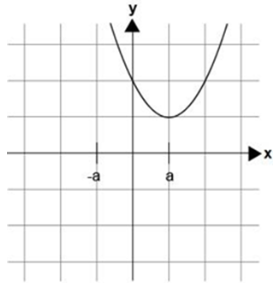
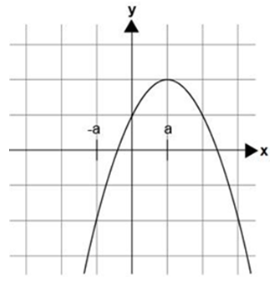
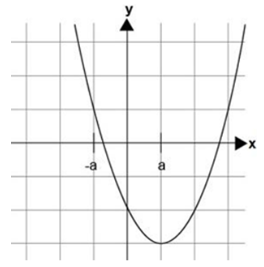
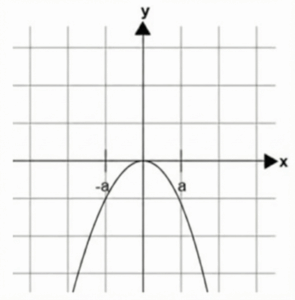
¿Cuál de las siguientes gráficas representa correctamente la función?
f(x) = ax^2 - 2ax + 2a