Hemos creado este simulacro de matemáticas de 22 reactivos de la guía de la UNAM para el área 4 para que pongas a prueba tus conocimientos previo al examen de admisión a la UNAM.

El área 4 corresponde a las carreras de las humanidades y de las artes de la UNAM, su principal característica es que abarca 10 temas, a diferencia de las otras tres áreas que en total son 9.
[no_toc]
Estructura examen área 4
El examen del área 4 tiene un total de 120 reactivos, y un tiempo de 3 horas para responderlo, es importante que tomes en cuenta que al ser un examen muy extenso en cantidad de temas debes de panificar bien tus tiempos de estudio.
Estructura examen de la UNAM para el área 4
| Materia | Reactivos |
| Español | 18 |
| Matemáticas | 22 |
| Física | 10 |
| Química | 10 |
| Biología | 10 |
| Historia universal | 10 |
| Historia de México | 10 |
| Literatura | 10 |
| Geografía | 10 |
| Filosofía | 10 |
Temario matemáticas UNAM área 4
El Área 4 abarca casi todas las materias que cursaste durante el bachillerato, por lo que repasar todos y cada uno de ellos puede tomarte mucho tiempo si no cuentas con los conocimientos básicos.
Estos son los temas que tienes que estudiar:
- Operaciones con números reales, complejos y expresiones algebraicas
- Números reales
- Suma y resta
- Multiplicación y división
- Raíces y potencias con exponente racional
- Números complejos
- Suma y resta
- Multiplicación
- Expresiones algebraicas
- Suma y resta
- Multiplicación y división
- Raíces y potencias con exponente racional
- Operaciones con radicales
- Números reales
- Productos notables y factorización
- Binomio de Newton a+bn, n ∈N
- Teorema del residuo y del factor
- Simplificación de fracciones algebraicas
- Operaciones con fracciones algebraicas
- Ecuaciones
- Ecuación, identidad y propiedades de la igualdad
- Ecuaciones de primer grado
- Ecuaciones de segundo grado
- Desigualdades
- Desigualdad de primer grado en una variable y sus propiedades
- Sistemas de ecuaciones
- Sistemas de dos ecuaciones lineales con dos incógnitas
- Métodos de solución
- Sistemas de tres ecuaciones lineales con tres incógnitas
- Métodos de solución (Regla de Cramer)
- Sistemas de dos ecuaciones lineales con dos incógnitas
- Funciones algebraicas
- Dominio, contradominio y regla de correspondencia
- Rango o imagen
- Gráfica
- Implícitas y explícitas
- Crecientes y decrecientes
- Continuas y discontinuas
- Álgebra de funciones
- Trigonometría
- Trigonometría básica
- Medida de un ángulo (conversión de grados a radianes y de radianes a grados)
- Razones trigonométricas
- Resolución de triángulos rectángulos
- Ley de los Senos y Ley de los Cosenos
- Resolución de triángulos oblicuángulos
- Razones trigonométricas para un ángulo en cualquier cuadrante. Fórmulas de reducción
- Funciones trigonométricas
- El círculo trigonométrico
- Funciones trigonométricas directas
- Dominio y rango
- Periodo y amplitud
- Desfasamiento
- Asíntotas de la gráfica
- Trigonometría básica
- Funciones exponenciales y logarítmicas
- Dominio y rango
- Gráficas y asíntotas
- Recta
- Distancia entre dos puntos
- Coordenadas de un punto que divide a un segmento de acuerdo con una razón dada
- Pendiente de una recta
- Formas de la ecuación de la recta y su gráfica
- Condiciones de paralelismo y perpendicularidad
- Distancia de un punto a una recta
- Ecuaciones de las medianas, mediatrices y alturas de un triángulo. Puntos de intersección (ortocentro, circuncentro y baricentro)
- Circunferencia
- Circunferencia como lugar geométrico
- Formas ordinarias (canónica) y general de la ecuación de la circunferencia con centro en el origen
- Ecuación de la circunferencia con centro en (h, k) en las formas ordinaria y general
- Elementos de una circunferencia
- Parábola
- Parábola como lugar geométrico
- Formas ordinaria y general de la ecuación de la parábola cuando el vértice está en el origen y el eje focal coincide con alguno de los ejes coordenados
- Formas ordinaria y general de la ecuación de la parábola cuando el vértice está en un punto cualquiera del plano y eje focal paralelo a alguno de los ejes coordenados
- Elementos de una parábola
- Elipse
- Elipse como lugar geométrico
- Relación entre los parámetros a, b y c
- Formas ordinaria y general de la ecuación de la elipse con centro en el origen y eje focal sobre alguno de los ejes coordenados
- Formas ordinaria y general de la ecuación de la elipse con centro fuera del origen y eje focal paralelo a alguno de los ejes coordenados
- Elementos de una elipse
- Hipérbola
- Hipérbola como lugar geométrico
- Relación entre los parámetros de la hipérbola a, b y c
- Formas ordinaria y general de la ecuación de la hipérbola con centro en el origen y eje focal sobre alguno de los ejes coordenados
- Formas ordinaria y general de la ecuación de la hipérbola con centro fuera del origen y eje focal paralelo a alguno de los ejes coordenados
- Elementos de una hipérbola
- Ecuación general de segundo grado
- Las cónicas
- Ecuación general de segundo grado
- Criterios para identificar a la cónica que representa una ecuación de segundo grado
- Traslación de ejes
Reactivo 1: División de fracciones
¿Cuál es el resultado de dividir \frac{1}{10} entre -\frac{1}{2} ?
- -20
- -\frac{1}{20}
- -\frac{1}{5}
- - 5
Solución:
Para calcular el cociente entre dos fracciones, debemos tener en cuenta la ley de signos en la división de números reales. Tenemos un número positivo dividido por un número negativo, el resultado debe ser negativo: \left(+\right)÷\left(-\right)=\left(-\right) .
Por otro lado, la división puede hacerse en forma de fracción o lineal. Independientemente del cómo se escriba la operación, el resultado debe ser el mismo. Esta vez haremos el cociente en forma de fracción.
\frac{\frac{1}{10}}{-\frac{1}{2}}
Aplicamos la regla de la “doble tortilla” o “doble C”.
\frac{\frac{1}{10}}{-\frac{1}{2}}=-\frac{2*1}{1*10}=-\frac{2}{10}
Simplificamos la fracción.
-\frac{2}{10}=-\frac{1}{5}
Concluimos que: el resultado de dividir \frac{1}{10} entre -\frac{1}{2} es -\frac{1}{5} .
Comparando con las opciones, seleccionamos como correcta la C.
Reactivo 2: Operaciones con radicales
Calcula \sqrt{{25}^{3}}
- 25
- 125
- 225
- 625
Solución:
En primer lugar, simplificar el radical parece complejo porque el exponente 3 no tiene división exacta con el índice 2 de la raíz. Por tanto, aparenta ser necesario desarrollar la tercera potencia de 25 para determinar luego su raíz cuadrada.
Si pensamos en el 25, nos daremos cuenta que dicha cantidad es igual a elevar 5 al cuadrado 25={5}^{2} . Sustituyamos 25 por {5}^{2} dentro de la raíz.
\sqrt{{25}^{3}}=\sqrt{{\left({5}^{2}\right)}^{3}}
Ahora, podemos aplicar potencia de una potencia. Multiplicamos los exponentes del 5, 2 y 3.
\sqrt{{\left({5}^{2}\right)}^{3}}=\sqrt{{5}^{6}}
El número 6 es divisible entre 2, podemos entonces simplificar la raíz cuadrada.
\sqrt{{5}^{6}}={5}^{\frac{6}{2}}={5}^{3}
Solo queda desarrollar la potencia de 5 al cubo. Cinco al cuadrado es 25 y este último por 5 es 125, por tanto:
{5}^{3}=125
Concluimos indicando que:
\sqrt{{25}^{3}}=125
Respuesta correcta al problema: inciso B.
Guía UNAM: Consulta todos los temas del área 4
Reactivo 3: Producto de polinomios
Al realizar el siguiente producto de polinomios (y-1)(y+2) , resulta
- {y}^{2}+y-2
- {y}^{2}-2
- {y}^{2}+1
- {y}^{2}+2y-1
Solución:
El producto entre dos polinomios se realiza tomando al primero y aplicando distributiva con cada uno de los términos del segundo. Luego, se desarrollan las distributivas simples pendientes, agrupamos términos y simplificamos hasta llegar a la mínima expresión.
En este caso, escogemos a (y-1) como el polinomio a distribuir entre los términos de (y+2) . Es indiferente la elección, pues recuerda que la multiplicación es conmutativa.
\left(y-1\right)\left(y+2\right)=y\left(y-1\right)+2\left(y-1\right)
Desarrollamos las distributivas.
y\left(y-1\right)+2\left(y-1\right)={y}^{2}-y+2y-2
Simplificamos hasta la mínima expresión.
{y}^{2}-y+2y-2={y}^{2}+y-2
Concluimos que:
Al realizar el siguiente producto de polinomios (y-1)(y+2) , resulta {y}^{2}+y-2 .
La respuesta correcta se encuentra en el inciso A.
Conoce los pasos de registro a la convocatoria de la UNAM.
Reactivo 4: Operaciones algebraicas
Resuelve la siguiente operación algebraica
\frac{\left({x}^{2}-7x+12\right)}{\left({x}^{2}-16\right)\left(x-3\right)}- \frac{1}{x-3}
- \frac{1}{x+4}
- \frac{x-3}{x+4}
- \frac{x-4}{x-3}
Solución:
Para llevar la fracción algebraica a su mínima expresión, es necesario representar todo como el producto de factores primos (irreducibles). En este caso, solo hay dos expresiones que se pueden reducir: {x}^{2}-7x+12 y {x}^{2}-16 .
En la primera, podemos aplicar la fórmula de segundo grado o factorización de la forma {x}^{2}+bx+c . Por simplicidad, nos favorece la segunda opción. Debemos encontrar dos números que sumados den -7 y multiplicados 12, ellos son: -3 y -4.
{x}^{2}-7x+12=\left(x-3\right)\left(x-4\right)
La expresión {x}^{2}-16 , puede factorizarse aplicando diferencia de cuadrados.
{x}^{2}-16={x}^{2}-{4}^{2}=\left(x+4\right)\left(x-4\right)
Sustituimos todo en la fracción original.
\frac{\left({x}^{2}-7x+12\right)}{\left({x}^{2}-16\right)(x-3)}=\frac{\left(x-3\right)\left(x-4\right)}{\left(x+4\right)\left(x-4\right)\left(x-3\right)}
Se simplifican x-3 y x-4 .
\frac{\left(x-3\right)\left(x-4\right)}{\left(x+4\right)\left(x-4\right)\left(x-3\right)}=\frac{1}{x+4}
Finalmente:
\frac{\left({x}^{2}-7x+12\right)}{\left({x}^{2}-16\right)(x-3)}=\frac{1}{x+4}
Concluimos seleccionando como correcta la opción B.
Reactivo 5: Fórmula de segundo grado
Cuando se sustituyen los valores de la ecuación de segundo grado 3{x}^{2}=2x+5 en la fórmula x=\frac{-b\pm \sqrt{{b}^{2}-ac}}{2a} , los valores a, b y c son
- a=3,b=2,c=5
- a=3,b=-2,c=5
- a=3,b=2,c=-5
- a=3,b=-2,c=-5
Solución:
Antes de emplear la fórmula de la resolvente de segundo grado, los términos del trinomio deben situarse en el primer miembro de la ecuación y la misma debe quedar igualada a cero. Procedemos a reordenar la ecuación.
3{x}^{2}=2x+5\to 3{x}^{2}-2x-5=0
Ahora, recordemos el orden que tienen los coeficientes en el trinomio de segundo grado.
a{x}^{2}+bx+c=0
Comparando con nuestra expresión, tenemos que:
a=3;b=-2;c=-5
Comparando esta correspondencia con las opciones de los incisos, la respuesta correcta se encuentra en el D.
Reactivo 6: Inecuaciones lineales
El conjunto solución de la desigualdad -3x+4>-8 es
- x\in \left(\frac{4}{3},\infty \right)
- x\in \left(-9,\infty \right)
- x\in \left(-\infty ,\frac{4}{3}\right)
- x\in \left(-\infty ,4\right)
Solución:
Calcular el conjunto solución de cualquier desigualdad lineal, se centra en dejar sola a la variable en el miembro izquierdo de la desigualdad, aplicando las reglas de las desigualdades.
-3x+4>-8
Restamos 4 en ambos miembros.
-3x+4-4>-8-4
-3x>-12
Ahora dividimos por -3. Como es un número negativo, el sentido de la desigualdad cambia a “<”.
-\frac{3x}{-3}<-\frac{12}{-3}
x<4
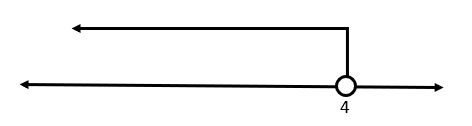
El conjunto solución de la desigualdad son todos los números menores que 4.
x\in \left(-\infty ,4\right)
La respuesta correcta se encuentra en el inciso D.
Oferta académica completa de la UNAM
Reactivo 7: Problemas con sistemas de ecuaciones lineales
Cinco cuadernos y ocho lapiceros cuestan $115; tres cuadernos y cinco lapiceros cuestan $70. ¿Cuál es el precio de cada cuaderno?
- $15
- $10
- $13
- $12
Solución:
Debemos extraer las ecuaciones de las frases en el enunciado. Luego de tener el SEL, podremos aplicar cualquier método para encontrar el precio de cada cuaderno. A los lapiceros los llamaremos l y a los cuadernos c .
Cinco cuadernos y ocho lapiceros cuestan $115.
5c+8l=115
Tres cuadernos y cinco lapiceros cuestan $70.
3c+5l=70
El sistema de ecuaciones quedaría como:
\left\{\begin{array}{c}5c+8l=115 \\ 3c+5l=70\end{array}\right.
Ya que solo nos interesa el precio de cada cuaderno, aplicaremos el método por sustitución para obtener una expresión únicamente en función de c . Despejamos a l de la primera ecuación.
5c+8l=115\to 8l=115-5c
l=\frac{115-5c}{8}
Sustituimos en la segunda ecuación.
3c+5\left(\frac{115-5c}{8}\right)=70
Multiplicamos todo por 8.
24c+5\left(115-5c\right)=560
24c+575-25c=560
Despejamos a c .
24c-25c=560-575
-c=-15
\therefore c=15
Concluimos indicando que el precio de cada cuaderno es de $15. La respuesta correcta está en el inciso A.
Reactivo 8: Dominio de funciones reales
¿Cuál es el dominio de la siguiente función polinomial?
f\left(x\right)={x}^{3}+2{x}^{2}-3x+1
- \left[-\infty ,\infty \right]
- (-\infty ,1)
- \left(-\infty ,\infty \right)
- (-1,\infty )
Solución:
El dominio de una función real, es el conjunto de valores de x para los cuales, se obtiene una imagen de f al ser evaluados en su regla de correspondencia.
Las funciones polinómicas tienen como dominio a todos los números reales. No importa el número que elijas, siempre tendrá una imagen finita y definida. Concluimos que: f\left(x\right)={x}^{3}+2{x}^{2}-3x+1 tiene como dominio a todos los números reales.
Dom\left(f\right)=x\in \left(-\infty ,\infty \right)
Al escribir conjuntos como intervalos, el infinito siempre se escribe con paréntesis porque no es un número real, solo una idea para representar subconjuntos que nunca terminan.
Seleccionamos como respuesta correcta la opción C.
Reactivo 9: Gráfica de una función real
La gráfica de {x}^{2}-1=y corresponde a una
- Recta
- Elipse
- Parábola
- Hipérbola
Solución:
La gráfica de una función polinómica (al igual que su clasificación) depende del mayor exponente de la variable. Si el exponente es 1, la gráfica será una recta, si es 2 (como en este caso) la gráfica será una parábola, si es 3 la gráfica es una “s” invertida con las puntas alargadas.
En base a este simple análisis, queda claro que la gráfica de la función y={x}^{2}-1 es una parábola con vértice en V\left(0,-1\right) .
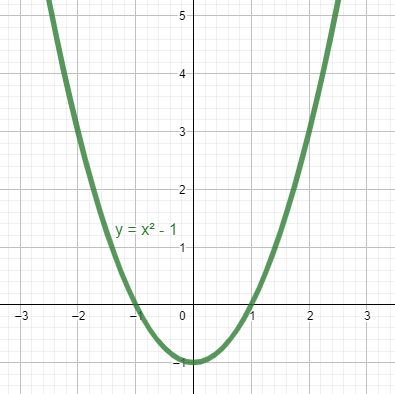
Respuesta correcta: inciso C.
Reactivo 10: Operaciones entre funciones
Determina el resultado de g\left(x\right)-f\left(x\right) , considerando:
f\left(x\right)=2x-3y+5 g\left(x\right)=7x+5y-11- 9x+2y-6
- 5x+8y-16
- 5x-8y+16
- 9x-2y+6
Solución:
Además de clasificar, graficar y describir el comportamiento de funciones, también podemos definir operaciones entre ellas, al igual que con los números o las expresiones algebraicas.
De hecho, para funciones en los números reales, las operaciones de suma, resta, multiplicación y división se desarrollan de la misma forma que para expresiones algebraicas. En resumen, sustituimos en el lugar correspondiente la regla de cada función, agrupamos términos semejantes y simplificamos.
\left(g-f\right)\left(x\right)=g\left(x\right)-f\left(x\right)
Sustituimos.
\left(g-f\right)\left(x\right)=7x+5y-11-\left(2x-3y+5\right)
\left(g-f\right)\left(x\right)=7x-2x+5y+3y-11-5=5x+8y-16
Concluimos entonces que:
g\left(x\right)-f\left(x\right)=5x+8y-16
Seleccionamos como respuesta correcta la opción B.
Reactivo 11: Problemas con trigonometría
Un edificio hace una sombra de 4 m con un ángulo de inclinación sobre el piso de 30°. ¿Cuál es la altura del edificio?
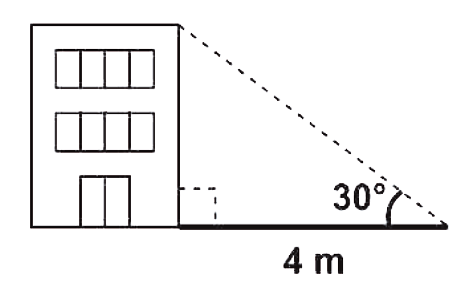
- \frac{4}{\sqrt{3}}m
- 2 m
- 8 m
- \frac{\sqrt{3}}{4}m
Solución:
Para calcular la altura del edificio debemos emplear alguna de las identidades trigonométricas presentes en un triángulo rectángulo. Conocemos el ángulo de 30° y el cateto adyacente a él, que corresponde a la sombra del edificio.
La altura del edificio corresponde con el cateto opuesto al ángulo de 30° y es nuestra incógnita en este caso. La identidad trigonométrica tangente de 30°, es igual al cociente entre el cateto opuesto y el cateto adyacente.
tan 30° =\frac{CO}{CA}=\frac{h}{4}
Donde h es la altura del edificio. Despejamos.
h=4tan 30° =\frac{4}{\sqrt{3}}
La altura del edificio es de \frac{4}{\sqrt{3}} metros.
Comparando con las opciones, seleccionamos como correcta la A.
Reactivo 12: Problemas con trigonometría
Un poste proyecta una sombra de 1.5 metros de longitud en el momento en el que el ángulo de elevación del sol es de 60°. ¿Cuál es la altura del poste?
Considera:
Sen {60}^{\circ }=\frac{\sqrt{3}}{2}
Cos {60}^{\circ } =\frac{1}{2}
Tan {60}^{\circ } =\sqrt{3}
- \frac{3\sqrt{3}}{2}m
- \frac{3}{4}m
- \frac{3}{8}m
- \frac{3\sqrt{3}}{4}m
Solución:
Hagamos un bosquejo rápido de la situación planteada en el enunciado.
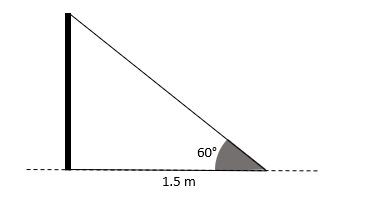
Respecto del ángulo de elevación de 60°, la sombra que mide 1.5 metros es el cateto adyacente y la altura desconocida del poste h es el cateto opuesto. Debido a que se forma un triángulo rectángulo, podemos aplicar la relación trigonométrica tangente en el ángulo de 60° para calcular a h .
tan 60 =\frac{CO}{CA}=\frac{h}{1.5}
Despejamos.
h=1.5tan 60 =\frac{3\sqrt{3}}{2}
Concluimos entonces que la altura del poste es de \frac{3\sqrt{3}}{2} metros.
La respuesta correcta al problema se encuentra en el inciso A.
¿Quieres practicar más? Simulacro de matemáticas de la UNAM
Reactivo 13: Dominio de una función real
Determina el dominio de la siguiente función.
f\left(x\right)=log\left(x\right)
- \left[0,\infty \right]
- (0,\infty ]
- [0,\infty )
- \left(0,\infty \right)
Solución:
La función logaritmo, en este caso base 10, acepta como argumento cualquier número que sea mayor o igual que cero. Es decir, la restricción que tiene la variable x dentro del logaritmo es que:
x>0
Escrito en notación de intervalo queda como:
x\in \left(0,\infty \right)
Concluimos seleccionando como respuesta correcta la opción D.
Reactivo 14: Dominio de una función real
Determina el dominio de la función
y=log(x-2)
- (2,\infty )
- [2,\infty )
- (-\infty ,2)
- (-\infty ,2]
Solución:
Para calcular el dominio de cualquier función real, debemos identificar las funciones básicas que forman parte de ella, establecer sus restricciones y resolver las respectivas inecuaciones, para finalmente interceptar en el conjunto solución total.
En este caso, la función está compuesta por un solo término cuya función principal es un logaritmo de base 10 (sabemos que es base 10 porque no se indica en el subíndice). La restricción para el argumento de cualquier logaritmo, es que sea mayor que cero, por tanto:
x-2>0
Resolvemos la inecuación.
x-2+2>2
\therefore x>2
El dominio de log(x-2) son todos los números mayores que 2.
D\left\{log(x-2)\right\}=\left(2,\infty \right)
La respuesta correcta se encuentra en el inciso A.
Reactivo 15: Distancia entre dos puntos
Calcula la distancia entre los puntos P(-\mathrm{1,1}) y Q(1,-1) en el plano cartesiano.
- \sqrt{8}
- 2
- \sqrt{2}
- 4
Solución:
La distancia entre dos puntos en el plano cartesiano se calcula con la siguiente fórmula:
d\left(P,Q\right)=\sqrt{{\left({x}_{p}-{x}_{q}\right)}^{2}+{\left({y}_{p}-{y}_{q}\right)}^{2}}
Donde:
\left({x}_{p},{y}_{p}\right)=\left(-\mathrm{1,1}\right)
\left({x}_{q},{y}_{q}\right)=\left(1,-1\right)
Sustituimos.
d\left(P,Q\right)=\sqrt{{\left(-1-1\right)}^{2}+{\left(1+1\right)}^{2}}
Resolvemos.
d\left(P,Q\right)=\sqrt{{\left(-1-1\right)}^{2}+{\left(1+1\right)}^{2}}=\sqrt{{2}^{2}+{2}^{2}}=\sqrt{8}
d\left(P,Q\right)=\sqrt{8}=2.82842
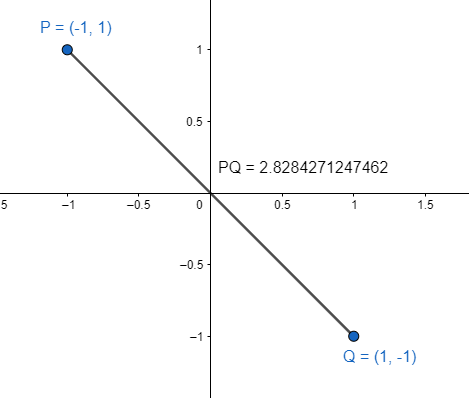
Concluimos indicando como respuesta correcta la opción A.
Reactivo 16: Distancia entre dos puntos
Calcula la distancia entre los puntos A\left(\mathrm{1,1}\right) y B\left(-1,-1\right) en el plano cartesiano.
- 2\sqrt{2}
- 5\sqrt{2}
- 2
- 4
Solución:
La distancia entre dos puntos en el plano real se calcula con la siguiente fórmula:
d\left(A,B\right)=\sqrt{{\left({x}_{a}-{x}_{b}\right)}^{2}+{\left({y}_{a}-{y}_{b}\right)}^{2}}
Donde:
\left({x}_{a},{y}_{a}\right)=\left(\mathrm{1,1}\right)
\left({x}_{b},{y}_{b}\right)=\left(-1,-1\right)
Sustituimos.
d\left(A,B\right)=\sqrt{{\left(1+1\right)}^{2}+{\left(1+1\right)}^{2}}
Resolvemos.
d\left(A,B\right)=\sqrt{{\left(1+1\right)}^{2}+{\left(1+1\right)}^{2}}=\sqrt{{2}^{2}+{2}^{2}}=\sqrt{8}
d\left(A,B\right)=\sqrt{8}=2\sqrt{2}
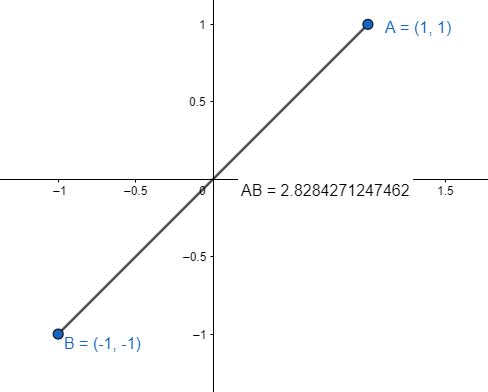
Concluimos indicando como respuesta correcta la opción A.
Reactivo 17: Ecuación de la circunferencia
¿Cuál de las siguientes ecuaciones corresponde a una circunferencia con centro en el origen y radio 2?
- {x}^{2}+{y}^{2}-4=0
- {x}^{2}-{y}^{2}-2=0
- {x}^{2}+{y}^{2}+2=0
- {x}^{2}-{y}^{2}-4=0
Solución:
Partimos de la ecuación ordinaria de la circunferencia con centro en \left(h,k\right) y radio r .
{\left(x-h\right)}^{2}+{\left(y-k\right)}^{2}={r}^{2}
En este caso, el centro tiene coordenadas \left(h,k\right)=\left(\mathrm{0,0}\right) y el radio una longitud r=2 unidades. Sustituimos los valores en la ecuación.
{\left(x-0\right)}^{2}+{\left(y-0\right)}^{2}={2}^{2}
{x}^{2}+{y}^{2}=4
Finalizamos pasando el 4 al primer miembro.
{x}^{2}+{y}^{2}-4=0
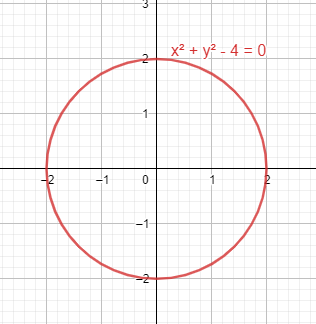
Seleccionamos como respuesta correcta la opción A.
Reactivo 18: Ecuación de la circunferencia
Ecuación que corresponde a una circunferencia de radio r=\sqrt{2} y centro en C\left(\mathrm{0,0}\right) .
- {x}^{2}-{y}^{2}=\sqrt{2}
- {x}^{2}+{y}^{2}=\sqrt{2}
- {x}^{2}-{y}^{2}=2
- {x}^{2}+{y}^{2}=2
Solución:
Para determinar la ecuación de la circunferencia, debemos sustituir en la expresión ordinaria de la circunferencia los parámetros correspondientes al centro y radio.
{\left(x-h\right)}^{2}+{\left(y-k\right)}^{2}={r}^{2}
En este caso C\left(h,k\right)=\left(\mathrm{0,0}\right) y r=\sqrt{2} . Sustituimos.
{\left(x-0\right)}^{2}+{\left(y-0\right)}^{2}={\left(\sqrt{2}\right)}^{2}
Desarrollamos.
{x}^{2}+{y}^{2}=2
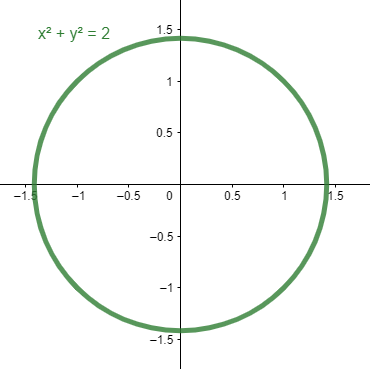
Comparando con las opciones, seleccionamos como correcta la D.
Reactivo 19: Ecuación de la parábola
La expresión x=4{y}^{2}+8y+2 , geométricamente representa una:
- Circunferencia
- Hipérbola
- Elipse
- Parábola
Solución:
Inspeccionando la forma de la ecuación, queda claro que debe pertenecer a una parábola, ya que solo una de las incógnitas se encuentra elevada al cuadrado. Específicamente, corresponde a una parábola con eje focal paralelo al eje de las x .
Para comprobar nuestra hipótesis, aplicaremos completación de cuadrados al segundo miembro.
x=4{y}^{2}+8y+2
Dividimos entre 4.
\frac{1}{4}x={y}^{2}+2y+\frac{1}{8}
Ya que el coeficiente de y es 2 y en el desarrollo del producto notable {\left(a+b\right)}^{2}={a}^{2}+2ab+{b}^{2} , corresponde al término 2ab , la única opción es que b=1 . Sumamos y restamos 1.
\frac{1}{4}x={y}^{2}+2y+1-1+\frac{1}{8}
\frac{1}{4}x={y}^{2}+2y+1-\frac{7}{8}
Ahora, aplicamos el producto notable {\left(a+b\right)}^{2} de forma inversa a {y}^{2}+2y+1 .
\frac{1}{4}x={\left(y+1\right)}^{2}-\frac{7}{8}
Pasamos el \frac{7}{8} al segundo miembro y extraemos factor común \frac{1}{4} .
\frac{1}{4}x+\frac{7}{8}={\left(y+1\right)}^{2}
\frac{1}{4}\left(x+\frac{7}{2}\right)={\left(y+1\right)}^{2}
Esta expresión corresponde a una parábola que abre paralela al eje x .
4p\left(x-h\right)={\left(y-k\right)}^{2}
Cuyo vértice \left(h,k\right)=\left(-\frac{7}{2},-1\right) .
Concluimos entonces que la respuesta correcta está en el inciso D.
Reactivo 20: Centro de la elipse
Determina el centro de una elipse con la siguiente ecuación.
\frac{(x-2{)}^{2}}{144}+\frac{(y-1{)}^{2}}{64}=1
- \left(\mathrm{8,12}\right)
- \left(\mathrm{2,1}\right)
- \left(\mathrm{1,2}\right)
- \left(\mathrm{12,8}\right)
Solución:
La elipse dada por el enunciado se encuentra expresada en su forma ordinaria, en ella se encuentran las coordenadas del centro \left(h,k\right) y los parámetros a y b elevados al cuadrado en el denominador de los binomios.
\frac{{\left(x-h\right)}^{2}}{{a}^{2}}+\frac{{\left(y-k\right)}^{2}}{{b}^{2}}=1
Por simple inspección, las coordenadas del centro para la elipse dada son:
C\left(h,k\right)=\left(\mathrm{2,1}\right)
Escogemos como respuesta correcta la opción B.
Reactivo 21: Lugares geométricos
Lugar geométrico en el plano cartesiano en el que el valor absoluto de la diferencia de sus distancias a dos puntos fijos en el mismo plano resulta siempre igual a una constante, positiva y menor que la distancia entre dichos puntos fijos.
- Circunferencia
- Parábola
- Elipse
- Hipérbola
Solución:
En este caso, debemos conocer las definiciones relacionadas con el lugar geométrico que representa cada cónica. Ya que el enunciado indica que la distancia medida es respecto a dos puntos fijos, podemos inferir que se trata de los focos de una elipse o una hipérbola.
Ahora, el lugar geométrico de una elipse corresponde al punto que se mueve en un mismo plano y cuya suma de las distancias medidas respecto a los focos es igual a una constante.
\left|{F}_{1}P\right|+\left|{F}_{2}P\right|=2a
\left|{F}_{1}{F}_{2}\right|>2a
Por otro lado, la hipérbola describe al punto cuyo valor absoluto de la diferencia de las distancias respecto a los focos, es igual a una constante y menor que la distancia entre los focos.
\left|\left|{F}_{1}P\right|-\left|{F}_{2}P\right|\right|=2a
\left|{F}_{1}{F}_{2}\right|<2a
Basados en todo este análisis, concluimos que la respuesta correcta está en el inciso D.
Reactivo 22: Ecuación de la cónica
¿Qué tipo de cónica representa la ecuación {y}^{2}+4x+2y+16=0 ?
- Parábola con vértice en el origen
- Elipse con centro fuera del origen
- Elipse con centro en el origen
- Parábola con vértice fuera del origen
Solución:
Con solo inspeccionar la ecuación, es fácil darse cuenta que se trata de una parábola, con eje focal paralelo a las x y con vértice fuera del origen porque están presente otros términos además de {y}^{2} y x .
Podemos comprobar nuestra suposición aplicando completación de cuadrados sobre la variable que está elevada al cuadrado, en este caso y .
{y}^{2}+4x+2y+16=0
Agrupamos las variables por miembro.
{y}^{2}+2y+16=-4x
Completamos cuadrado sumando y restando 1 del lado de las y .
{y}^{2}+2y+1-1+16=-4x
{y}^{2}+2y+1+15=-4x
Pasamos el 15 al segundo miembro y aplicamos producto notable.
{y}^{2}+2y+1=-4x-15
{\left(y+1\right)}^{2}=-4\left(x+\frac{15}{4}\right)
Es una parábola que abre paralela al eje x , con dirección hacia la izquierda y vértice en \left(-\frac{15}{4},-1\right) fuera del origen.
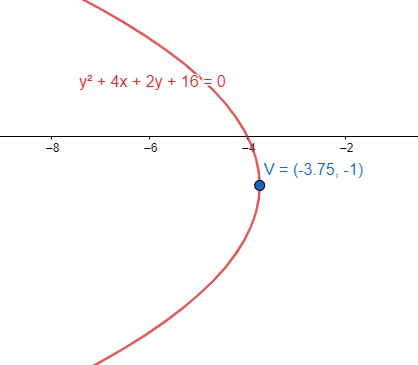
Comparando con las opciones, la respuesta correcta está en el inciso D.

