¡Felicidades aspirante! Llegamos a la cuarta y última parte de la guía de pensamiento matemático IPN 2023, correspondiente a los reactivos desde el 31 al 40.

Continúa estudiando el resto de asignaturas con el material que hemos preparado en la zona de materiales IPN. No olvides incorporar exámenes simulacro en tus jornadas de estudio, monitorea tus tiempos y perfecciónalos antes de la prueba de ingreso.
Reactivo 31
En la Riviera Maya, un ingeniero civil diseñó un hotel de 5 niveles cuya forma es piramidal. La planta baja, que es de base cuadrada, tiene un área de 1050m2. Por otra parte, la altura entre un nivel y el siguiente es de 3 m, con una inclinación de 60°. ¿Cuántos metros cuadrados mide el quinto nivel?
- 890 {\mathrm{m}}^{2}
- 1010 {\mathrm{m}}^{2}
- 990 {\mathrm{m}}^{2}
- 1015 {\mathrm{m}}^{2}
Solución:
Para resolver el problema debemos tener presente un par de cosas. Primero, que la inclinación se refiere al ángulo que tienen las caras triangulares de la pirámide respecto a la base cuadrada.
Por otra parte, los pisos cuadrados son concéntricos y se cuentan de la siguiente forma: planta baja, nivel 1, nivel 2, …, nivel 5. Hagamos una representación bidimensional de la pirámide, vista de manera frontal desde una de sus caras.
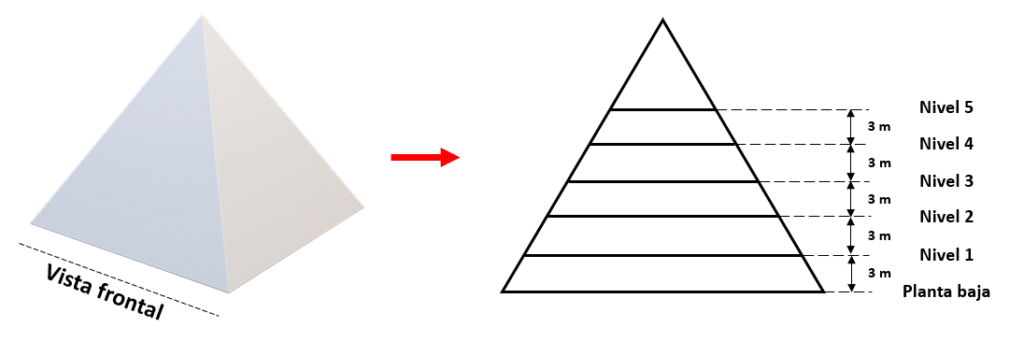
Ahora, para calcular el área de un cuadrado, solo debemos conocer el valor de su lado. El enunciado nos indica el área que ocupa la base, con esta información podemos obtener las dimensiones de la planta baja.
{l}_{pb}=\sqrt{{A}_{pb}}=\sqrt{1050 {\mathrm{m}}^{2}}=32.4 \mathrm{m}
Si examinamos la figura anterior, vemos que existe una distancia de separación entre los lados de la base y los lados del nivel 5. Si calculamos esta distancia y la restamos con la base, obtenemos el lado del quinto nivel.
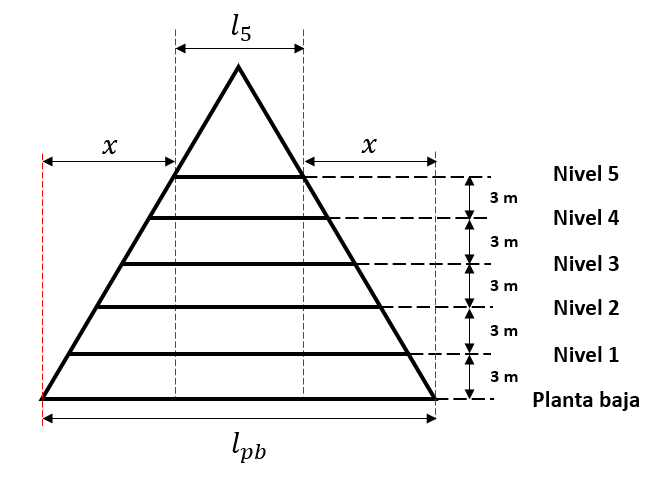
{l}_{5}={l}_{pb}-2x
El valor de x se puede calcular aplicando trigonometría. Conocemos la altura desde la base hasta el nivel 5 y sabemos que el ángulo que se forma es de 60°.
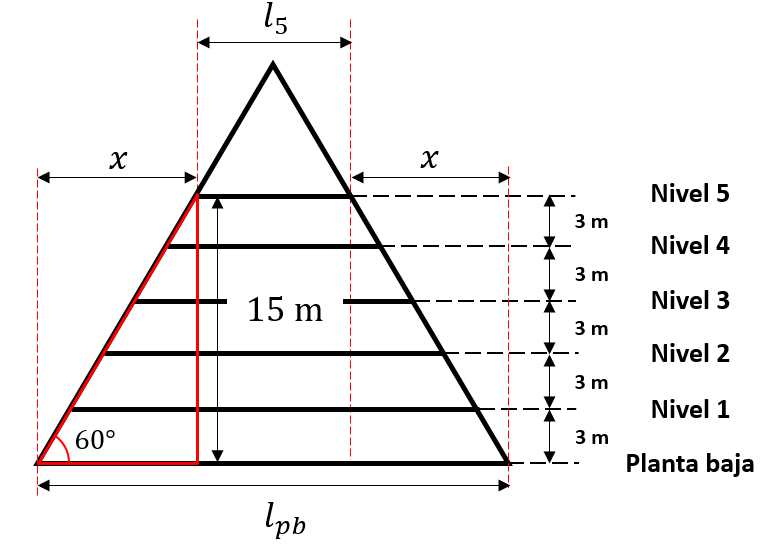
Con la tangente de 60° podemos calcular a x .
\mathrm{tan}60=\frac{15}{x}\to x=\frac{15}{\mathrm{tan}60}
\therefore x=8.66 \mathrm{m}
Sustituimos en la ecuación de {l}_{5} .
{l}_{5}=32.4-2\left(8.66\right)=15.08 \mathrm{m}
Finalmente, el área del nivel 5 se obtiene como:
{A}_{5}={l}_{5}^{2}={\left(15.08\right)}^{2}=227.4 {\mathrm{m}}^{2}
El área del nivel 5 es de 227.4 metros cuadrados. En este reactivo hay un error en los incisos, ninguno corresponde a la respuesta correcta.
Reactivo 32
Dentro de una nave industrial se construye un contenedor cilíndrico. Si la altura máxima disponible en la nave es de 1000 cm y se necesita espacio para contener un volumen de 2000 m3, ¿cuál es el radio que debe tener el cilindro?
- 5\sqrt{\frac{8}{\pi }} \mathrm{m}
- \sqrt{\frac{2}{\pi }} \mathrm{m}
- \sqrt{20}\pi \mathrm{m}
- 2\sqrt{\frac{8}{5}}\pi \mathrm{m}
Solución:
Sabemos que el volumen de un cilindro se calcula como:
{V}_{cil}=\pi {r}^{2}h
Donde h es la altura del cilindro. Convertimos la altura a metros antes de sustituirla en la ecuación.
1000 \mathrm{c}\mathrm{m}\cdot \frac{1 \mathrm{m}}{100 \mathrm{c}\mathrm{m}}=10 \mathrm{m}
La altura del contenedor cilíndrico es de 10 metros. Despejamos el radio.
{r}^{2}=\frac{{V}_{cil}}{\pi h}\to r=\sqrt{\frac{{V}_{cil}}{\pi h}}
Sustituimos los valores en la ecuación.
r=\sqrt{\frac{2000}{\pi \left(10\right)}}=\sqrt{\frac{200}{\pi }}=5\sqrt{\frac{8}{\pi }} \mathrm{m}
El radio del contenedor cilíndrico debe ser de 5\sqrt{\frac{8}{\pi }} metros.
Indicamos como respuesta correcta al inciso a).
Reactivo 33
Una esfera que almacena combustible en PEMEX está llena a una tercera parte. Sin embargo, un operador mide el perímetro P=24\pi \mathrm{m} de la sombra central que produce la esfera al medio día.
¿Cuál es el volumen de combustible almacenado en {\mathrm{m}}^{3} ?
- 250\pi {\mathrm{m}}^{3}
- 768\pi {\mathrm{m}}^{3}
- 1254\pi {\mathrm{m}}^{3}
- 2304\pi {\mathrm{m}}^{3}
Solución:
La sombra central a la que se refiere el enunciado, equivale a mirar el tanque esférico desde la vista superior.
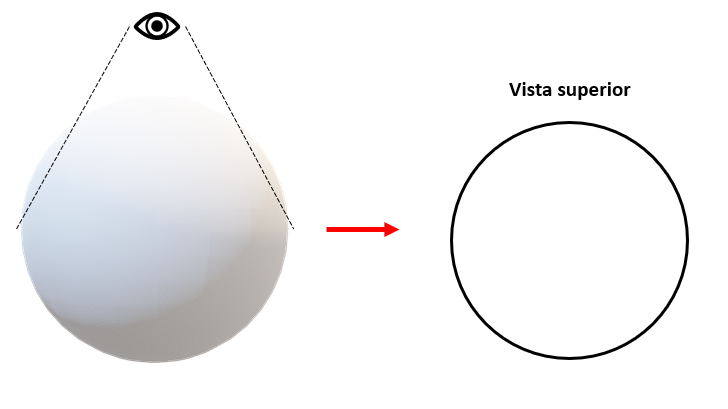
A partir del perímetro de esta sombra podemos calcular el radio de la esfera.
p=2\pi r\to r=\frac{p}{2\pi }
Sustituimos.
r=\frac{24\pi }{2\pi }=12 \mathrm{m}
Calculamos el volumen total de la esfera como:
{V}_{e}=\frac{4}{3}\pi {r}^{3}=\frac{4}{3}\pi {\left(12\right)}^{3}=2304\pi {\mathrm{m}}^{3}
Finalmente, obtenemos el volumen almacenado dividiendo al volumen total por 3.
{V}_{al}=\frac{2304\pi }{3}=768\pi {\mathrm{m}}^{3}
La respuesta correcta es el inciso b).
Reactivo 34
El taller mecánico le cobró a Marta $1200 pesos. Por el servicio de rutina pagó 1/6 de esa suma, mientras que la compostura de los frenos costó 3/10 del resto del monto. En la factura también se registró el cambio del embrague. ¿Cuánto pagó Marta por esta compostura?
- $700
- $750
- $800
- $840
Solución:
Nota: el enunciado tiene un error en la pregunta, realmente solicita calcular el valor del cambio de embrague, no de la compostura porque esta se calcula de forma directa.
El costo total del servicio mecánico que pagó Marta es igual a la suma del costo del servicio de rutina, la compostura y el cambio de embrague.
P={P}_{sr}+{P}_{c}+{P}_{ce}
El servicio de rutina es la decimosexta parte del pago total.
{P}_{sr}=\frac{1200}{6}=200 \mathrm{\$}
Por otra parte, la compostura costó 3/10 del resto del monto. Es decir, el pago de la compostura es igual a multiplicar 1200$ menos el servicio de rutina por 3/10.
{P}_{c}=\frac{3}{10}\left(1200-200\right)=300 \mathrm{\$}
Con esto, despejamos el costo del cambio de embrague de la suma total.
{P}_{ce}=P-{P}_{sr}-{P}_{c}=1200-200-300=700 \mathrm{\$}
El costo del cambio de embrague fue de 700 pesos.
La respuesta correcta es el inciso a).
Reactivo 35
Tres aviones (A1, A2 y A3) salen del aeropuerto de la Ciudad de México según esta rutina: el primero lo hace cada 12 horas; el segundo, cada 18 horas y el tercero cada 30 horas. Sin embargo, en algún momento las tres salidas coinciden. ¿Cada cuánto tiempo ocurre esto y cuántas veces habrá despegado cada avión antes de que los tres vuelvan a coincidir?
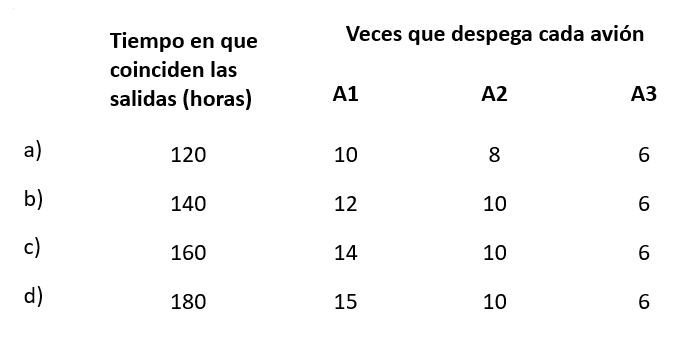
Solución:
Para resolver este problema, solo debemos calcular el mínimo común múltiplo de los tres períodos de tiempo.
\mathrm{m}\mathrm{c}\mathrm{m}\left(12, 18, 30\right)=180 \mathrm{h}\mathrm{o}\mathrm{r}\mathrm{a}\mathrm{s}
Los aviones coinciden en sus salidas cada 180 horas. Esta información es suficiente para concluir que la respuesta correcta es el inciso d).
Reactivo 36
Un sistema de tratamiento de agua utiliza 3 filtros de carbono para limpiar 120 litros. ¿Cuántos filtros se requieren para tratar 520 litros de agua?
- 9
- 13
- 17
- 21
Solución:
Aplicamos una regla de tres directa para resolver el problema. Debe ser directa, porque a mayor volumen de agua, se debe disponer de una mayor cantidad de filtros.
\frac{x}{520}=\frac{3}{120}\to x=\frac{\left(3\right)\left(520\right)}{120}=13 \mathrm{f}\mathrm{i}\mathrm{l}\mathrm{t}\mathrm{r}\mathrm{o}\mathrm{s}
En el sistema de tratamiento necesitamos 13 filtros para tratar los 520 litros de agua.
Indicamos como respuesta correcta al inciso b).
Reactivo 37
Cuál es el precio final de una mercancía importada cuyo valor es de $3,000 pesos si, en su reventa, se quiere ganar 3/10 de su costo original.
- $4050
- $3900
- $2500
- $3750
Solución:
Al precio de compra al mayor, le sumamos el margen de ganancia de 3/10 respecto al valor de adquisición de la mercancía.
PV=3000+3000\left(\frac{3}{10}\right)=3900\$
El precio de venta es de 3900 pesos.
La respuesta correcta es el inciso b).
Reactivo 38
Con base en la tabla, calcular el porcentaje de matrimonios en los que la edad de la mujer comprende entre 30 y 34 años.
Consulta de matrimonios por edad de la mujer según la edad del hombre.
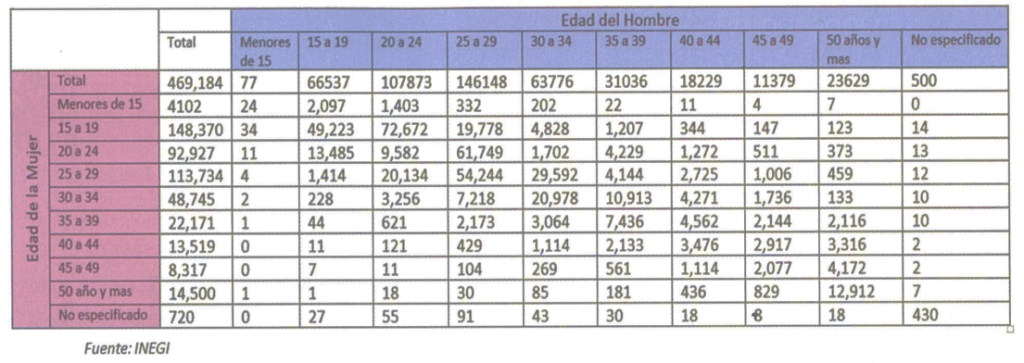
- 3%
- 6%
- 10%
- 15%
Solución:
Para calcular el porcentaje solicitado, debemos identificar el número de matrimonios respecto al rango de edades de la mujer, sumar el total de matrimonios y luego dividir ambas cantidades.
En la columna 6, en la zona identificada como “Edades de la mujer”, tenemos que el total de matrimonios en el rango de 30 a 34 años es de 48745, mientras que el total de matrimonios es de 469184.
{\left[30-34\right]}_{\%}=\frac{48745}{469184}\cdot 100\%=10.4\%
Comparando con los incisos, concluimos que la respuesta correcta es c).
Reactivo 39
Según la gráfica, ¿en qué año empiezan a decrecer los fallecimientos por enfermedades infecciosas?
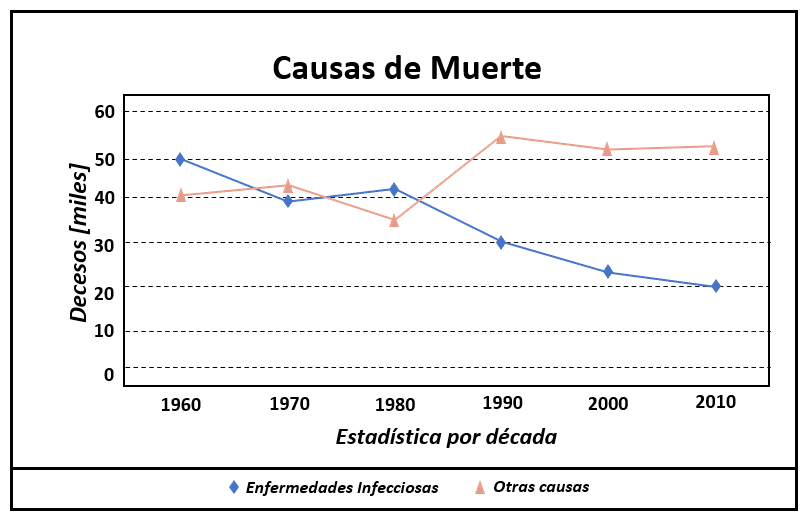
- 1990
- 1980
- 1970
- 1960
Solución:
Examinando la gráfica, podemos concluir sin mayor análisis que a partir del año 1980 las muertes por enfermedades infecciosas comienzan a decrecer de forma sostenida en el tiempo.
En el año 1970 aunque hay una disminución, esta viene a ser una corrección en el número de muertes por enfermedades infecciosas. Concluimos entonces que la respuesta correcta es el inciso b).
Reactivo 40
De acuerdo con la gráfica, para el nivel básico se contrató a 51,574 profesores en Oaxaca. ¿Cuál es el total de profesores contratados en el nivel superior?
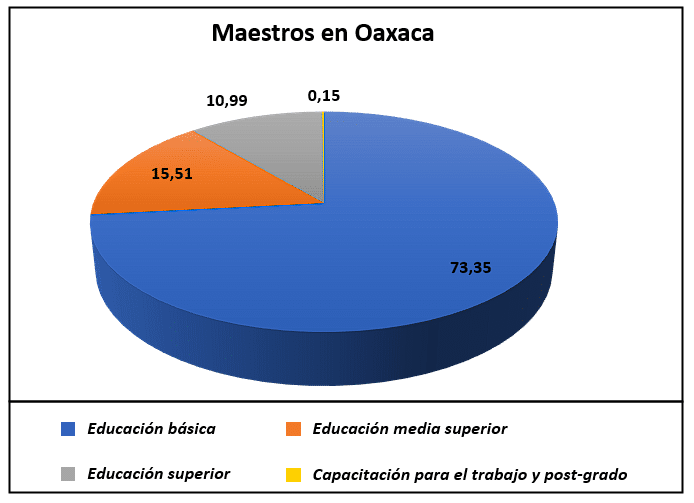
- 5668
- 7857
- 10905
- 12670
Solución:
Gracias al enunciado conocemos el total de profesores contratados para educación básica y el porcentaje que representan del total, por otra parte sabemos que el porcentaje de profesores de nivel superior es 10.99%.
Aplicamos una regla de tres para calcular el total de profesores contratados para nivel superior.
73.35\to 51574
10.99\to x
Resolviendo nos queda:
x=\frac{\left(51574\right)\left(10.99\right)}{73.35}=7727 \mathrm{p}\mathrm{r}\mathrm{o}\mathrm{f}\mathrm{e}\mathrm{s}\mathrm{o}\mathrm{r}\mathrm{e}\mathrm{s}
Se contrató un total de 7727 profesores para nivel superior.
El único inciso que parece acercarse al cálculo es el b), pero la guía señala que el correcto es el inciso a). Podemos estar seguros de que se trata de un error de redacción, porque ninguno de los porcentajes del gráfico equivale a 5668.

