Guía IPN 2023 Pensamiento Matemático | Parte 2 resuelta

Continuamos con la solución de la nueva guía de estudios para el examen de ingreso en la parte de pensamiento matemático, en esta segunda parte vamos a resolver los ejercicios del 11 al 20.

Recuerda intentar resolver los ejercicios por tu cuenta antes de consultar la solución del reactivo correspondiente.

Reactivo 11

Identificar los elementos octavo y noveno de la sucesión siguiente:

1,\frac{1-\sqrt{2}}{2}, \frac{1+\sqrt{3}}{2}, -\frac{1}{2}, \dots 

1. \frac{1}{2}-\sqrt{2} y 2
2. \frac{1+\sqrt{8}}{2} y \frac{1}{2}-\sqrt{2}
3. \frac{1-2\sqrt{8}}{2} y 2\sqrt{2}
4. \frac{1}{2}+\sqrt{2} y 2

Solución:

Debido a que en el enunciado solo se visualizan los primero 4 términos de la sucesión, para calcular el octavo y noveno elemento es conveniente obtener primero la fórmula general de la sucesión.

Comprobamos que sea una sucesión aritmética calculando la diferencia entre términos adyacentes.

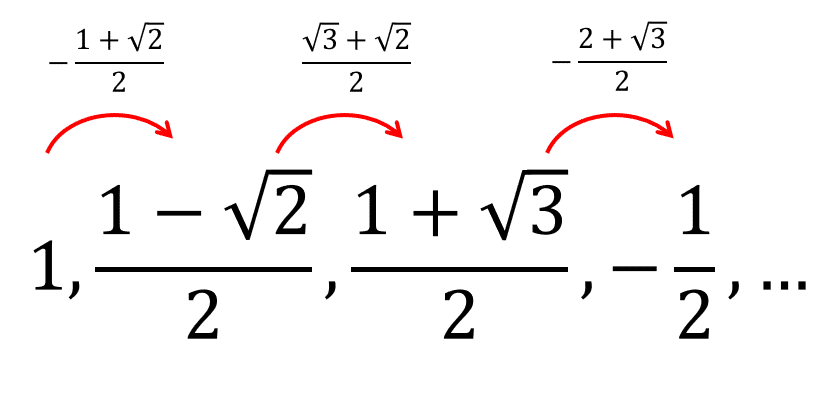
La sucesión no es aritmética porque la diferencia no es constante. La sucesión tampoco es geométrica, porque la razón \frac{{a}_{2}}{{a}_{1}}=\frac{1-\sqrt{2}}{2} pero la de \frac{{a}_{3}}{{a}_{2}}=\frac{1+\sqrt{3}}{1-\sqrt{2}} . La ley de cambio entre términos es alternante.

Vemos que en el numerador de los términos 2 y 3, el radical cambia de -\sqrt{2} a +\sqrt{3} . Si aplicamos esta lógica en el primer y cuarto término, los radicales en estos casos deberían ser: +\sqrt{1} y -\sqrt{4} , radicales que dan como resultado a los valores de los términos.

{a}_{1}=\frac{1+\sqrt{1}}{2}=\frac{1+1}{2}=1

{a}_{4}=\frac{1-\sqrt{4}}{2}=\frac{1-2}{2}=-\frac{1}{2}

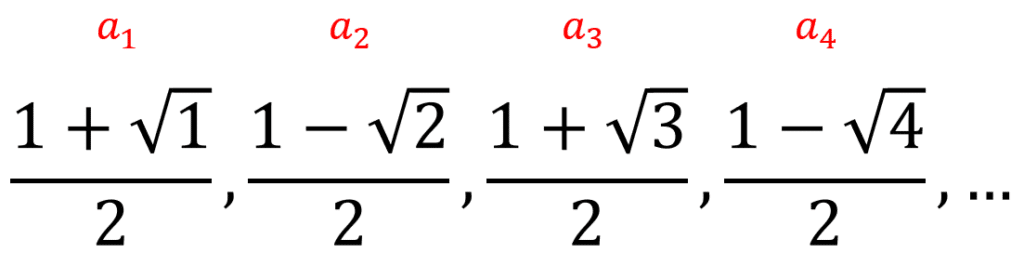
Llegados a este punto, podemos resolver el ejercicio encontrando de forma directa a los términos octavo y noveno. Veamos que el radicando corresponde al valor de n mientras que el signo es positivo cuando n es impar y negativo cuando es par.

Teniendo en cuenta esto, el valor de {a}_{8} y {a}_{9} sería:

{a}_{8}=\frac{1-\sqrt{8}}{2},{a}_{9}= \frac{1+\sqrt{9}}{2}\to {a}_{8}=\frac{1-2\sqrt{2}}{2},{a}_{9}= 2

{a}_{8}=\frac{1}{2}-\sqrt{2},{a}_{9}= 2

Comparando con los incisos, concluimos que la respuesta correcta se encuentra en la opción a).

\frac{1+\sqrt{1}}{2},\frac{1-\sqrt{2}}{2},\frac{1+\sqrt{3}}{2},\frac{1-\sqrt{4}}{2}, \frac{1+\sqrt{5}}{2},\frac{1-\sqrt{6}}{2},\frac{1+\sqrt{7}}{2},\frac{1-\sqrt{8}}{2},\frac{1+\sqrt{9}}{2},\dots 

Reactivo 12

Determinar los primeros 5 elementos de la sucesión que tiene la fórmula general:

{s}_{n}=\frac{{\left(-1\right)}^{n}n\cdot \left(n-1\right)}{2n+1}

Para n=1, 2, 3, \dots 

1. \frac{1}{3},\frac{2}{5},\frac{6}{7},\frac{12}{3}, -\frac{20}{11}
2. \frac{1}{3},\frac{2}{5},-\frac{6}{7},\frac{4}{3}, -\frac{20}{11}
3. 0,\frac{2}{5},-\frac{6}{7},\frac{4}{3}, -\frac{20}{11}
4. 0,\frac{2}{5},\frac{6}{7},\frac{4}{3}, -\frac{20}{11}

Solución:

Sustituimos los valores de n dados por el enunciado en la expresión del término general.

{s}_{1}=\frac{{\left(-1\right)}^{1}\left(1\right)\cdot \left(1-1\right)}{2\left(1\right)+1}=\frac{\left(-1\right)\left(0\right)}{3}=0

Solo los incisos c) y d) comienzan por 0. Debemos encontrar hasta el tercer elemento para distinguir cual es el correcto.

{s}_{2}=\frac{{\left(-1\right)}^{2}\left(2\right)\cdot \left(2-1\right)}{2\left(2\right)+1}=\frac{\left(1\right)\left(2\right)\left(1\right)}{5}=\frac{2}{5}

{s}_{3}=\frac{{\left(-1\right)}^{3}\left(3\right)\cdot \left(3-1\right)}{2\left(3\right)+1}=\frac{\left(-1\right)\left(3\right)\left(2\right)}{7}=-\frac{6}{7}

Tenemos que la sucesión es:

{s}_{n}=\left\{0,\frac{2}{5}, -\frac{6}{7}, \dots \right\}

Comparando entre c) y d), la respuesta correcta es el inciso c).

Reactivo 13

Identificar la secuencia que reproduce el término general siguiente:

{a}_{n}=\frac{{\left(-1\right)}^{2n+1}}{2}\mathrm{cos}\left(n\pi \right)+\frac{{\left(-1\right)}^{2n}}{2}\mathrm{sin}\left(\frac{4n+1}{2}\pi \right)

Considerar valores de: n= 0, 1, 2, 3,\dots 

1. 0, -\frac{1}{2},0, 1, 0, -2, \dots
2. 0, -1, 0, -1, 0, -1, \dots
3. 0, \frac{1}{2},0, 1, 0, 2, \dots
4. 0, 1, 0, 1, 0, 1, \dots

Solución:

Sustituimos los valores dados de n hasta que podamos identificar la respuesta correcta entre los incisos. Recordemos que el coseno de n\pi  es igual a \pm 1 y que el seno es \pm 1 para múltiplos de \frac{\pi }{2} .

{a}_{0}=\frac{{\left(-1\right)}^{2\left(0\right)+1}}{2}\mathrm{cos}\left(0\right)+\frac{{\left(-1\right)}^{2\left(0\right)}}{2}\mathrm{sin}\left(\frac{1}{2}\pi \right)=\left(-\frac{1}{2}\right)\left(1\right)+\left(\frac{1}{2}\right)\left(1\right)=0

{a}_{1}=\frac{{\left(-1\right)}^{2\left(1\right)+1}}{2}\mathrm{cos}\left(\pi \right)+\frac{{\left(-1\right)}^{2\left(1\right)}}{2}\mathrm{sin}\left(\frac{5}{2}\pi \right)=\left(-\frac{1}{2}\right)\left(-1\right)+\left(\frac{1}{2}\right)\left(1\right)=\frac{1}{2}+\frac{1}{2}=1

{a}_{n}=\left\{0, 1, \dots \right\}

Con los dos primeros términos y examinando los incisos, podemos concluir que la respuesta correcta es el d).

Reactivo 14

Calcular cuatro números impares consecutivos cuya suma sea 352.

1. 81, 85, 89, 97
2. 81, 87, 91, 93
3. 85, 87, 88, 92
4. 85, 87, 89, 91

Solución:

Teniendo en cuenta los incisos y que los impares deben ser consecutivos, descartamos a las opciones a, b y c, porque los números impares no son consecutivos (la distancia entre elementos es distinta a 2) o hay términos que son pares (por ejemplo, en el inciso c).

Comprobamos que la suma de los términos en el inciso d sea 352.

S=85+87+89+91

\mathrm{S}=172+89+91

\mathrm{S}=261+91=352

Finalmente, la respuesta correcta es el inciso d).

Reactivo 15

Identificar la expresión general que reproduce la sucesión:

4, -12, 36, -108, 324, ...

Para valores de n=1, 2, 3,\dots 

1. {a}_{n}={\left(-4\right)}^{n}{3}^{n-1}
2. {a}_{n}=-4{\left(-1\right)}^{n-1}{4}^{n}
3. {a}_{n}=-4{\left(-1\right)}^{n}{3}^{n-1}
4. {a}_{n}=-3{\left(-1\right)}^{n}{4}^{n-1}

Solución:

Lo primero que se puede identificar al examinar los términos de la sucesión, es que los elementos son alternantes, con signo positivo para las posiciones impares. Esto se logra multiplicando al término general por el factor: {\left(-1\right)}^{n-1} .

{\left(-1\right)}^{n-1}=\left\{1, -1, 1, -1, \dots \right\}

El único término con este factor es el b), pero está multiplicado por -4, provocando que la secuencia cambia a -1, 1, -1, 1,\dots  Descartamos esta opción. Los candidatos pasan a ser c y d, porque {\left(-1\right)}^{n}=\left\{-1, 1, -1, 1,\dots \right\} pero con el menos de afuera quedan \left\{1, -1, 1, -1, \dots \right\} .

Comprobamos calculando el primer elemento de ambas expresiones.

Término general c.

{a}_{1}=-4{\left(-1\right)}^{1}{3}^{1-1}=\left(-4\right)\left(-1\right)\left(1\right)=4

Término general d.

{a}_{1}=-3{\left(-1\right)}^{1}{4}^{1-1}=\left(-3\right)\left(-1\right)\left(1\right)=3

La respuesta correcta es el inciso c).

Reactivo 16

Completar la secuencia:

III, IX, ____, LXXXI, ____, DCCXXIX, …

1. XXIIV y CCIIIXL
2. XXVII y CCXLIII
3. XXIIV y CCXCIII
4. XXVIII y CCLIII

Solución:

La secuencia del enunciado está expresada en números romanos, la convertimos a números arábigos para identificar la posible secuencia.

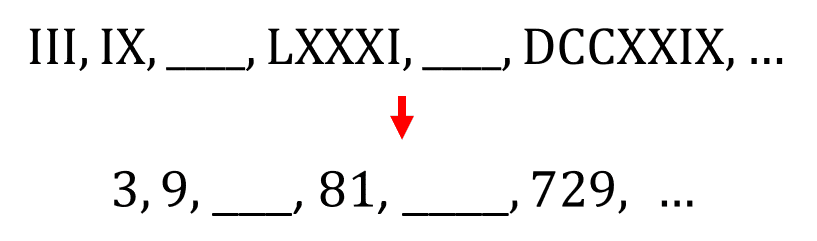
Ahora, vemos que la sucesión evoluciona multiplicando por 3 al elemento actual para obtener al siguiente.

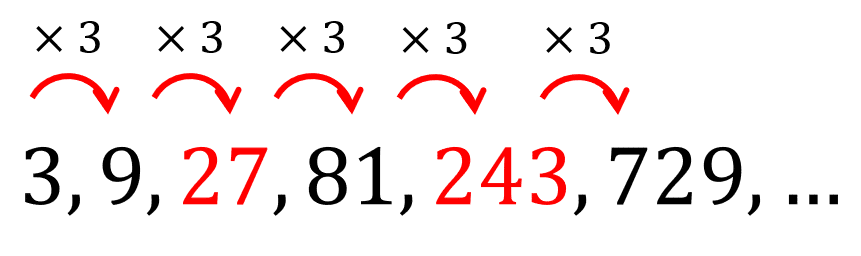
Los elementos que completan a la sucesión son 27 y 243 . Expresados en números romanos:

27=\mathrm{X}\mathrm{X}\mathrm{V}\mathrm{I}\mathrm{I}

243=\mathrm{C}\mathrm{C}\mathrm{X}\mathrm{L}\mathrm{I}\mathrm{I}\mathrm{I}

Comparando con las opciones del problema, concluimos que la correcta es b).

Reactivo 17

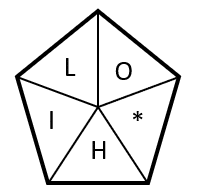
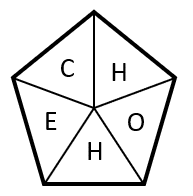
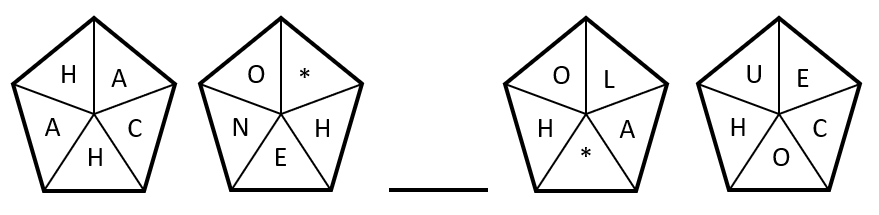
Completar la secuencia con la figura correcta.

1. 
2. 
3. 
4. 

Solución:

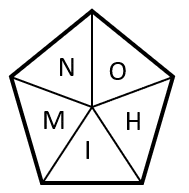
Examinando las figuras de la secuencia gráfica, identificamos cuatro características importantes. La primera, es que todas son palabras que comienzan por H: HACHA, HENO, …

Por otra parte, las palabras son de 5 o 4 letras, alternadas con esa secuencia: 5 letras, 4 letras, 5 letras … Tanto la “H” como el asterisco que ocupa el lugar vacío en las palabras con 4 letras, se desplazan dos posiciones en sentido horario.

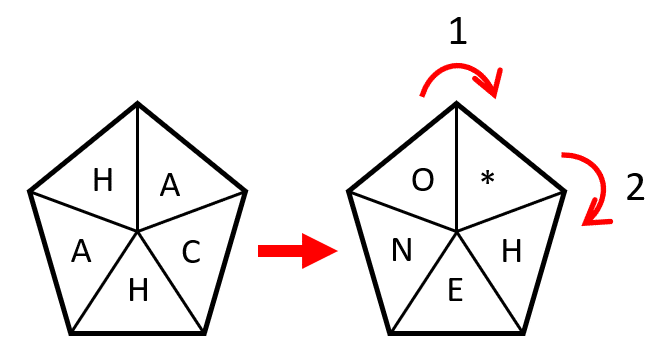
Luego permanece en la misma posición cuando la palabra es de 5 letras y se vuelve a desplazar 2 posiciones para la siguiente palabra de 4 letras. Finalmente, la primera vocal de cada palabra es una letra del vocabulario.

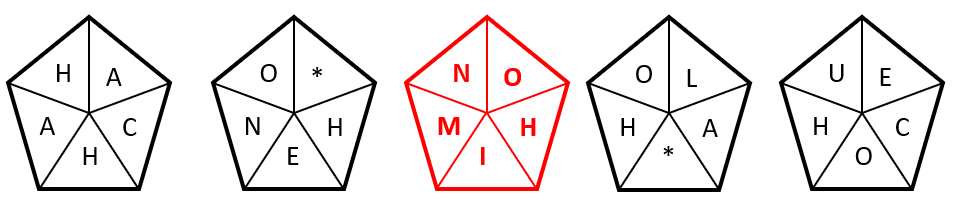
HACHA, HENO, ____, HOLA, HUECO

Teniendo en cuenta estas características, la “H” debe estar en el lugar actual, debe ser una palabra de 5 letras y la vocal de la primera sílaba debe ser “I”. Examinando a los incisos, la respuesta correcta es el d).

HACHA, HENO, HIMNO, HOLA, HUECO

Reactivo 18

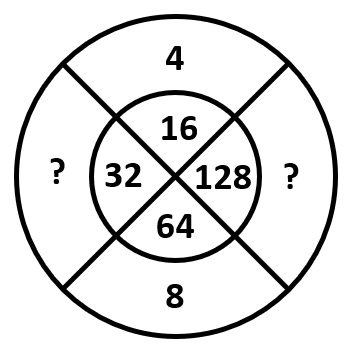
Identificar los números que faltan en la secuencia del arreglo considerando un orden que va de izquierda a derecha.

1. 4 y 32
2. 6 y 10
3. 6 y 8\sqrt{2}
4. 4\sqrt{2} y 8\sqrt{2}

Solución:

Examinando la figura, podemos identificar que los números en el círculo interior en la misma línea que el 4 y el 8, se obtienen al elevar dichas cantidades al cuadrado.

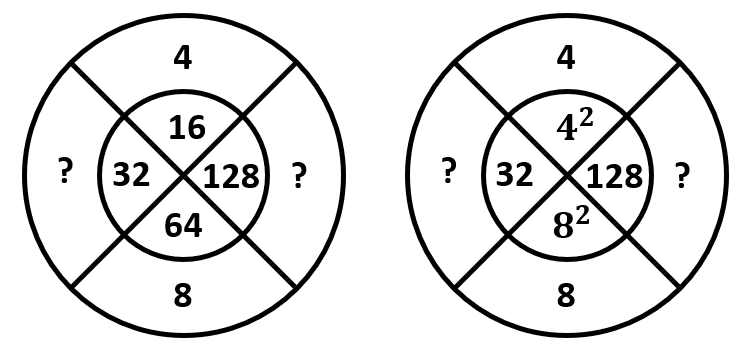
Siguiendo esta lógica, los números desconocidos deben ser la raíz cuadrada de 32 y 128 respectivamente. Examinando a los incisos, si elevamos al cuadrado 4\sqrt{2} y 8\sqrt{2} , obtenemos 32 y 128.

{\left(4\sqrt{2}\right)}^{2}=16\cdot 2=32

{\left(8\sqrt{2}\right)}^{2}=64\cdot 2=128

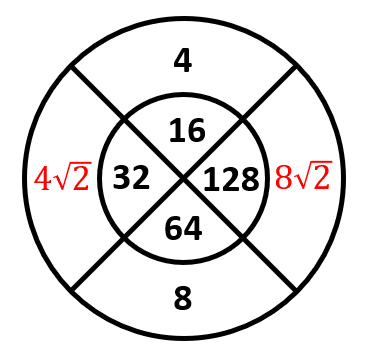
Seleccionamos como respuesta correcta al inciso d).

Reactivo 19

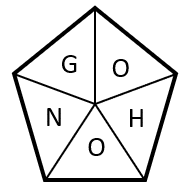
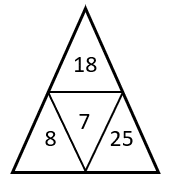
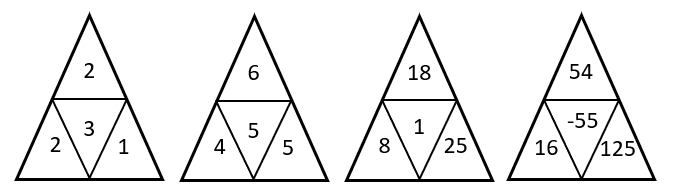
¿Qué triángulo falta en la siguiente secuencia?

1. 
2. 
3. 
4. 

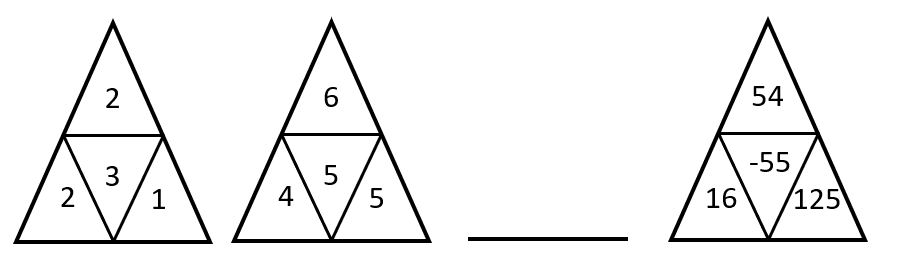
Solución:

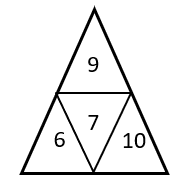
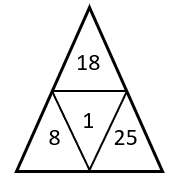
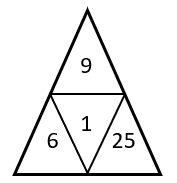
Para determinar la figura que completa la serie gráfica, debemos identificar la ley de cambio entre los números de los triángulos. Los números en el triángulo superior evolucionan multiplicando al actual por 3.

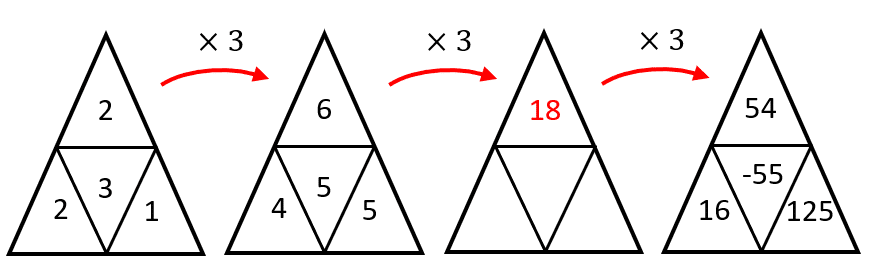
Aplicando el mismo razonamiento, los números en el triángulo inferior izquierdo evolucionan multiplicando por 2, mientras que los del triángulo inferior derecho se multiplican por 5.

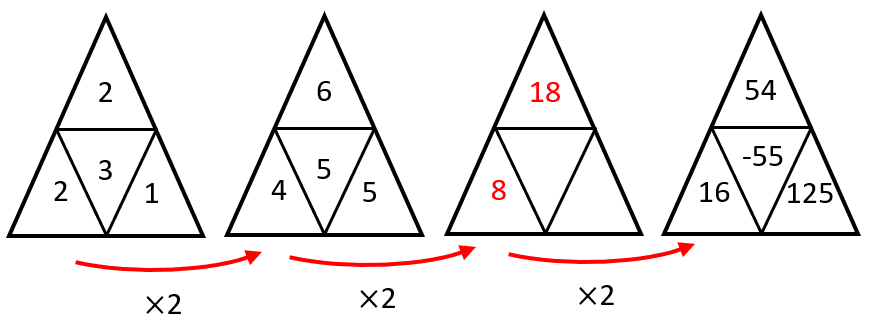
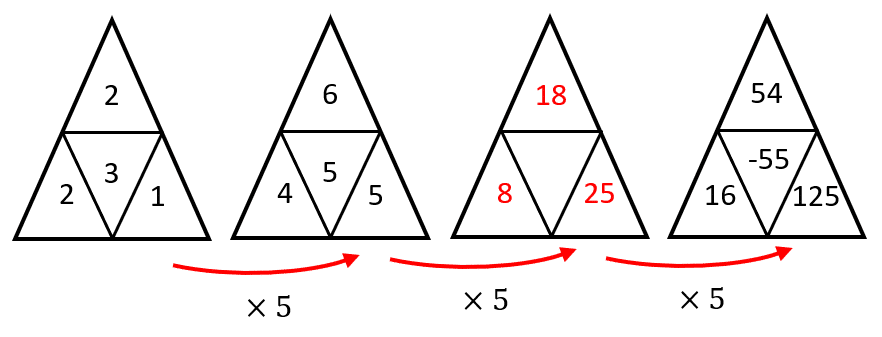
Con esta información, podemos descartar a los incisos a y c.

Por otra parte, el número del centro se encuentra sumando el triángulo izquierdo con el superior, para luego restarlo con el número del triángulo derecho.

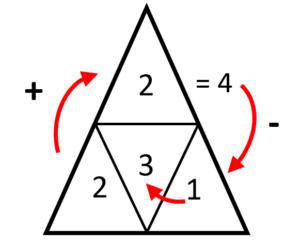
Aplicando esto en la figura obtenemos:

{T}_{c}=8+18-25=1

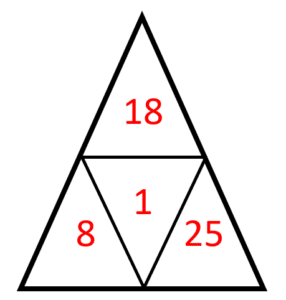
Concluimos indicando como respuesta correcta al inciso b).

Reactivo 20

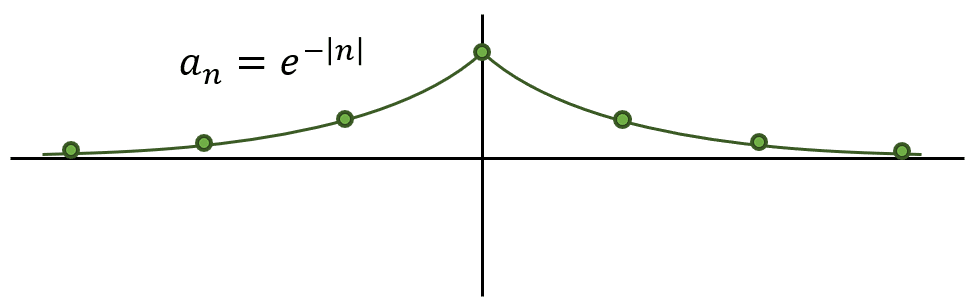
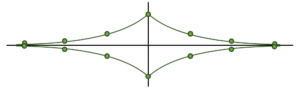
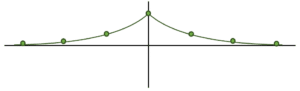
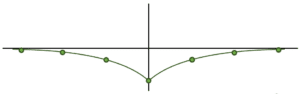
¿Qué secuencia de puntos en el plano reproduce el término general {a}_{n}={e}^{-\left|n\right|} ?

Para n= 0, 1, 2, \dots 

1. 
2. 
3. 
4. 

Solución:

Para seleccionar la gráfica que representa a la sucesión, debemos analizar al término general considerando las propiedades de los exponentes y del valor absoluto.

Cuando se aplica valor absoluto a una cantidad, el resultado de la operación será el mismo número, pero de signo positivo. Por otro lado, una potencia con signo negativo se puede escribir como:

{a}_{n}={e}^{-\left|n\right|}=\frac{1}{{e}^{\left|n\right|}}

Teniendo en cuenta lo anterior, el resultado que se obtiene del término general es siempre positivo. El máximo valor se obtiene para n=0 y los resultados decrecen de manera asintótica hacia cero a medida que n aumenta o decrece de valor.

Esto último es porque tenemos el cociente de 1 sobre un número cada vez más grande, el resultado será un número cada vez más pequeño. La gráfica que representa lo anterior es la del inciso c).