Examen Simulador EXANI II Pensamiento Matemático V.3 P.3

Llegamos a la parte final del examen simulacro de pensamiento matemático del Exani II en la tercera versión. ¿Ya resolviste las otras partes? En este tutorial vamos a resolver los ejercicios del 21 al 30.

Recuerda desarrollarlos por tu cuenta antes de revisar la solución.

Puedes continuar estudiando para tu examen de ingreso con los materiales EXANI II que tenemos para ti.

Reactivo 21

Suponga que las ecuaciones que definen a las curvas de la figura forman un sistema de dos ecuaciones con dos incógnitas ¿Cuál es la solución de dicho sistema de ecuaciones?

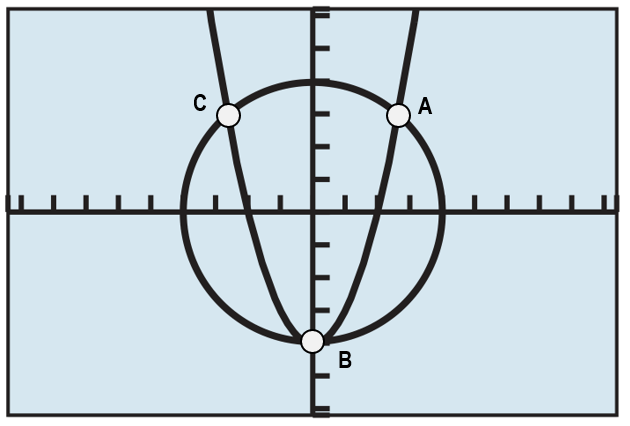
1. No hay solución
2. La solución es C y A
3. La solución es A, B y C

Solución:

En geometría analítica, cuando se desea conocer los puntos de intersección entre dos figuras, se toman sus respectivas ecuaciones para formar un sistema de ecuaciones. La solución de dicho sistema corresponde a los puntos de intersección que se desean conocer.

Geométricamente, esto se entiende como encontrar los puntos que son comunes entre ambos lugares geométricos. En esta línea de ideas y comparando con las opciones, seleccionamos como correcta la opción c).Añadid

Reactivo 22

Determine el valor de {\mathrm{cot}}^{2}\theta  sabiendo que \mathrm{cos}\theta =\frac{1}{2} .

1. {\mathrm{cot}}^{2}\theta =1
2. {\mathrm{cot}}^{2}\theta =\frac{1}{3}
3. {\mathrm{cot}}^{2}\theta =\frac{7}{3}

Solución:

Comencemos por indicar la relación trigonométrica básica de la cotangente:

\mathrm{cot}\theta =\frac{\mathrm{cos}\theta }{\mathrm{sin}\theta }

Elevamos todo al cuadrado.

{\mathrm{cot}}^{2}\theta =\frac{{\mathrm{cos}}^{2}\theta }{{\mathrm{sin}}^{2}\theta }

Empleamos la identidad pitagórica para sustituir seno cuadrado en función de coseno cuadrado.

{\mathrm{sin}}^{2}\theta +{\mathrm{cos}}^{2}\theta =1\to {\mathrm{sin}}^{2}\theta =1-{\mathrm{cos}}^{2}\theta 

Sustituimos:

{\mathrm{cot}}^{2}\theta =\frac{{\mathrm{cos}}^{2}\theta }{1-{\mathrm{cos}}^{2}\theta }

Ahora, sustituimos el valor de coseno al cuadrado.

{\mathrm{cot}}^{2}\theta =\frac{{\left(\frac{1}{2}\right)}^{2}}{1-{\left(\frac{1}{2}\right)}^{2}}=\frac{\frac{1}{4}}{\frac{3}{4}}=\frac{1}{3}

\therefore {\mathrm{cot}}^{2}\theta =\frac{1}{3}

Comparando con las opciones, la respuesta correcta es la b).

Reactivo 23

Suponga una que tiene una parábola con eje focal paralelo al eje y . Si la ecuación de dicha parábola es {\left(x-h\right)}^{2}=4p\left(y-k\right) , ¿cómo se relaciona c con h , k y p ?

{\left(x-h\right)}^{2}=4p\left(y-k\right)\to y=a{x}^{2}+bx+c

1. c=\frac{{h}^{2}}{4p}+k
2. c={h}^{2}+k
3. c=4phk

Solución:

Para expresar a c en función de los parámetros h , k y p , debemos desarrollar y luego agrupar en términos semejantes a la ecuación {\left(x-h\right)}^{2}=4p\left(y-k\right) de la parábola.

Desarrollando la expresión.

{\left(x-h\right)}^{2}=4p\left(y-k\right)

{x}^{2}-2hx+{h}^{2}=4py-4pk

Agrupamos.

4py={x}^{2}-2hx+{h}^{2}+4pk

y=\frac{1}{4p}{x}^{2}-\frac{h}{2p}x+\frac{{h}^{2}}{4p}+k

Igualando coeficientes con y=a{x}^{2}+bx+c nos queda:

a=\frac{1}{4p};b=-\frac{h}{2p};c=\frac{{h}^{2}}{4p}+k

Comparando con las opciones, indicamos como la correcta a la a).

Reactivo 24

Se tiene un cuadrado como el que se muestra en la figura y solo se puede rotar 45° y 90° ¿Cuál de las siguientes afirmaciones de correcta?

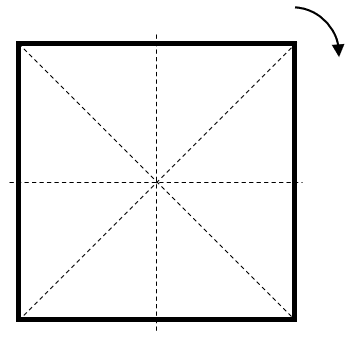
1. La figura permanece invariante cuando se rota 90°
2. La figura permanece invariante cuando se rota 45°
3. La figura no permanece invariante bajo ninguna rotación

Solución:

Para este problema, debemos probar rotar la figura 45° y 90°, e identificamos si permanece invariante, es decir, sigue siendo un cuadrado con lados horizontales y otros verticales. Rotamos primero 45°.

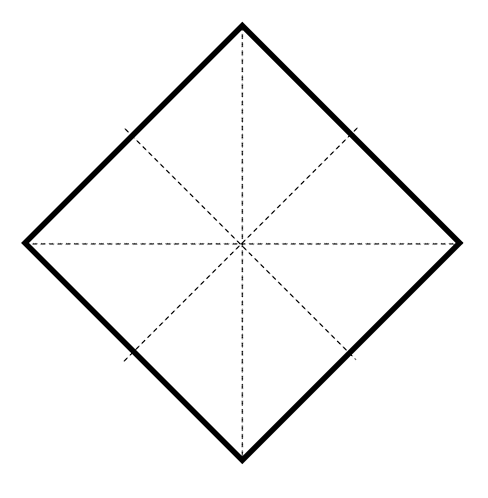
En este caso la figura no es la misma que antes de ejecutar la rotación. Probemos rotando 90°.

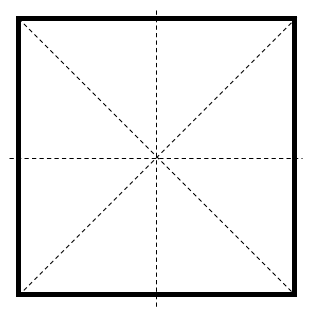
Con una rotación de 90° la figura es idéntica a la original. Concluimos que es invariante ante rotaciones de 90°.

Comparando con las opciones la respuesta correcta es la a).

Reactivo 25

El siguiente conjunto de datos corresponde a las unidades fabricadas por una empresa en los últimos 30 días. Si tuviera que establecer en un histograma de frecuencias estos datos, ¿cuál sería la forma más eficiente de representarlos?

\begin{array}{c}38\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}35\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}76\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}58\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}48\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}59\\ 67\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}63\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}33\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}69\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}53\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}51\\ 28\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}25\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}36\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}32\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}61\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}57\\ 49\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}78\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}48\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}42\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}72\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}52\\ 47\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}66\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}58\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}44\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}44\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}\hspace{0.25em}56\end{array}

1. En forma agrupada
2. En forma desagrupada
3. No sería posible representarlos en un histograma de frecuencias

Solución:

Debido a que la cantidad de datos es 30, un histograma de frecuencias o el cálculo de cualquier otro parámetro estadístico será complejo y tedioso. Por esta razón, es necesario expresar los datos de forma agrupada por intervalos.

Concluimos indicando como correcta la opción a).

Reactivo 26

En la tabla que se muestra a continuación, está representada la demanda de agua a través del tubo matriz de una central que suministra agua a una comunidad, en intervalos de 3 horas.

¿Qué tipo de función representan los datos de la tabla?

1. Lineal
2. Cuadrática
3. Cúbica

Solución:

Antes de graficar los puntos, podemos intentar un truco para comprobar si la grafica es lineal. Calculamos la pendiente entre 3 puntos consecutivos de los datos, si el resultado es al mismo, entonces la gráfica es una recta.

Tengamos en cuenta que el tiempo será la coordenada x y el caudal será la coordenada y .

{m}_{12}=\frac{7-6}{6-3}=\frac{1}{3}

{m}_{23}=\frac{8-7}{9-3}=\frac{1}{3}

La pendiente es igual, por tanto, concluimos que los datos representan una recta.

Comparando nuestro resultado con las opciones, seleccionamos como correcta la a).

Reactivo 27

El siguiente histograma de frecuencias establece la cantidad de hits ejecutados por un equipo durante los 9 innings de un partido de baseball. Indique cuál de las siguientes frases establece una comparación correcta.

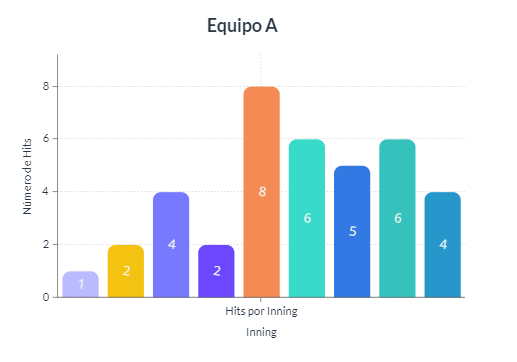
1. Desde el 5 inning, los jugadores batearon menos que en los innings anteriores
2. A partir del 5 inning, el equipo rindió por encima del promedio que tuvo en la primera parte del juego
3. No se puede emitir una comparación a partir del histograma

Solución:

Para responder correctamente, debemos examinar las frases de los incisos y comprobar su veracidad a partir del histograma.

Frase a: Desde el 5 inning, los jugadores batearon menos que en los innings anteriores.

Esto es falso, ya que, por el contrario, desde el 5 inning los jugadores comenzaron a tener mayor contacto a la hora de batear.

Frase b: A partir del 5 inning, el equipo rindió por encima del promedio que tuvo en la primera parte del juego.

Teniendo en cuenta lo dicho para la frase anterior, esta parece ser la correcta. Calculemos rápidamente la media de hits que tuvo el equipo.

\stackrel{-}{h}=\frac{1+2+4+3+8+6+5+6+4}{9}=4.22\approx 4

En efecto, el rendimiento del equipo durante la segunda parte del juego fue superior a la media.

Frase c: No se puede emitir una comparación a partir del histograma.

Esta frase es incorrecta, ya que si hemos extraído información útil desde el histograma.

Concluimos indicando que la respuesta correcta es la opción b).

Reactivo 28

¿Qué ocurre con la gráfica de una parábola cuyo parámetro a disminuye de valor en un factor \alpha  positivo? Tenga en cuenta que:

a{x}^{2}+bx+c\to \frac{a}{\alpha }{x}^{2}+bx+c

\alpha >0

1. Se desplaza verticalmente hacia arriba
2. Se desplaza horizontalmente hacia la derecha
3. Crece el lado recto de la parábola

Solución:

El coeficiente a de una parábola se relaciona con los parámetros h, k y p de la siguiente manera:

a=\frac{1}{4p}

Si dividimos el coeficiente a entre un numero \alpha >0 nos queda:

\frac{a}{\alpha }=\frac{1}{4p\alpha }

Es decir, que indirectamente estamos multiplicando a p por dicho factor \alpha >0 . Ya que p está directamente relacionado con el lado recto de la parábola, al aumentar p se ensancha la parábola.

En base a este análisis, podemos concluir que la respuesta correcta es la c).

Reactivo 29

Una empresa está por iniciar operaciones en una planta que acaban de construir, lo único que falta es seleccionar al encargado de control de calidad para que lleve a cabo la operación exitosa de la planta. Para el puesto se han presentado ingenieros: Juan y Julia, ambos especialistas en control de calidad.

El criterio de selección debe ser estricto, por lo que ambos se someterán a prueba por 5 días y quien tenga la menor desviación respecto del patrón que se les ha proporcionado y cuya media de las desviaciones sea menor, tendrá el trabajo.

Condiciones:

Desviación estándar menor y media aritmética menor

Porcentaje de desviación de Julia y Juan respecto al patrón.

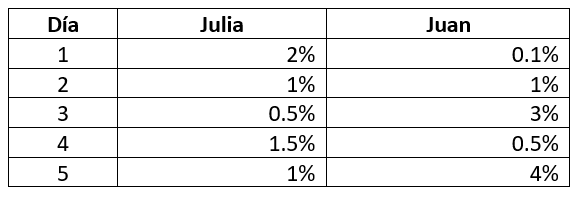
1. Juan
2. Julia
3. Ninguno cumple con las condiciones establecidas

Solución:

Para seleccionar a uno de los dos aspirantes, debemos calcular la media y la varianza de los datos suministrados por el enunciado. Comencemos por Julia.

Media aritmética de Julia.

{\stackrel{-}{x}}_{1}=\frac{2+1+0.5+1.5+1}{5}=1.2\%

Varianza de Julia.

{s}_{1}^{2}=\frac{\sum _{1}^{n} {\left({x}_{i}-\stackrel{-}{X}\right)}^{2}}{n}=\frac{{\left(1.2-2\right)}^{2}+{\left(1.2-1\right)}^{2}+{\left(1.2-0.5\right)}^{2}+{\left(1.2-1.5\right)}^{2}+{\left(1.2-1\right)}^{2}}{5}

{s}_{1}^{2}=\frac{1.3}{5}=0.26\%

Ahora con Juan.

Media aritmética de Juan.

{\stackrel{-}{x}}_{2}=\frac{0.1+1+3+0.5+4}{5}=1.72\%

Varianza de Julia.

{s}_{2}^{2}=\frac{\sum _{1}^{n} {\left({x}_{i}-\stackrel{-}{X}\right)}^{2}}{n}=\frac{{\left(1.72-0.1\right)}^{2}+{\left(1.72-1\right)}^{2}+{\left(1.72-3\right)}^{2}+{\left(1.72-0.5\right)}^{2}+{\left(1.72-4\right)}^{2}}{5}

{s}_{2}^{2}=\frac{11.47}{5}=2.29\%

Comparando los resultados, queda claro que Julia es quien cumple con las condiciones impuestas por la empresa.

Concluimos indicando que la respuesta correcta es la b).

Reactivo 30

Un grupo de biólogos se encuentra estudiando el crecimiento de una especie de planta que habita en zonas urbanas para relacionar esta característica con el nivel de contaminación del suelo, medida en porcentaje de nutrientes por micrómetro cúbico ( \frac{{\%}_{N}}{\mu {m}^{3}} ).

El banco de datos esta expresado en años. Una columna muestra los niveles de contaminación promedio y la otra, el porcentaje de crecimiento de las plantas, ambos como un promedio anual.

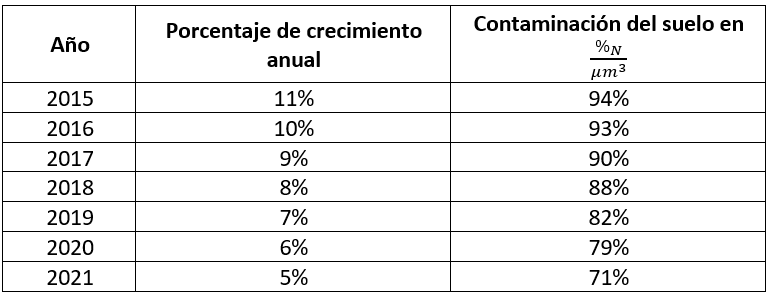
¿En qué año se presenta el mayor impacto de la contaminación sobre el crecimiento de las plantas?

Ayuda: la contaminación está dada en % de nutrientes, para hacer la comparación debe usar el % de contaminantes.

1. 2015
2. 2018
3. 2021

Solución:

Debido a que necesitamos medir el impacto de los contaminantes en el suelo sobre el crecimiento de las plantas, debemos calcular el porcentaje de contaminantes por año a partir de la tabla de datos. Agregamos otra columna que representa el porcentaje de contaminantes.

Dicho porcentaje de contaminantes lo calculamos como:

{\%}_{C}=100-{\%}_{N}

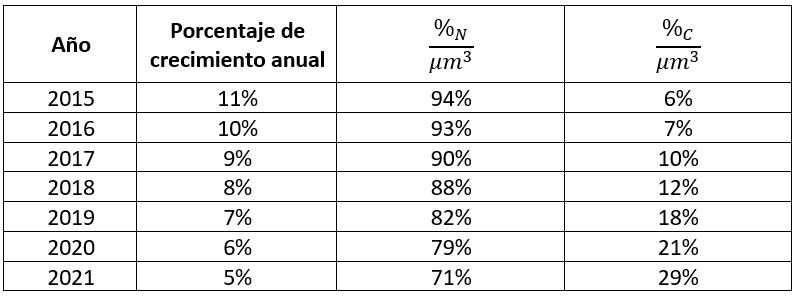
Ahora, hacemos el cociente entre el porcentaje de crecimiento anual {\%}_{Cre} y el porcentaje de contaminantes {\%}_{C} para obtener el impacto de la contaminación sobre el crecimiento.

\frac{{\%}_{Cre}}{{\%}_{C}}

Si es mayor que 1, el crecimiento ha prevalecido. Si es igual que 1, no hubo variación. Si es menor que 1, el crecimiento se vio afectado por la contaminación. Agregamos otra columna.

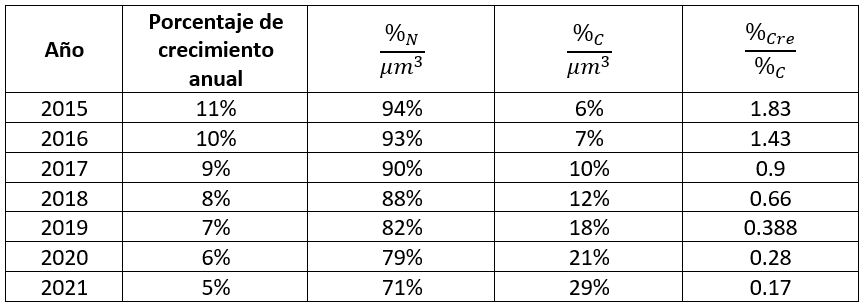
El año donde la contaminación tuvo mayor impacto sobre el crecimiento de las plantas fue en 2021.

Comparando con las opciones, seleccionamos como correcta la c).