Llegamos a la parte 6 del simulador de Matemáticas para el examen de admisión, y en esta ocasión toca un bloque que parece sencillo, pero que suele provocar muchos errores: segmentos y rectas en el plano cartesiano.

Este tema aparece una y otra vez en los exámenes de admisión, ya sea que vayas a presentar a la UNAM, al IPN o a una universidad que aplique el EXANI II.
No importa la carrera: distancia entre puntos, punto medio, pendiente y ecuaciones de rectas siempre vienen.
Si vienes de las partes anteriores, ya sabes cómo va esto: simuladores durante todo el ciclo previo al examen.
Y si eres nuevo por aquí, rápido contexto: esta es la sexta parte de una serie de prácticas diseñadas para que resuelvas exactamente el tipo de ejercicios que sí te preguntan el día del examen.
Temas del simulador
En esta parte vas a trabajar ejercicios de:
- Distancia entre dos puntos en el plano cartesiano.
- Punto medio de un segmento, incluyendo expresiones con variables.
- Pendiente de una recta a partir de su ecuación.
- Ecuación de medianas en triángulos.
- Distancia de un punto a una recta y distancia perpendicular.
Recomendaciones
Aquí es donde muchos aspirantes fallan, no por no saber la fórmula, sino por errores muy comunes como:
- Confundir el orden de los puntos al calcular la distancia.
- Promediar mal las coordenadas al obtener el punto medio.
- No despejar correctamente la ecuación para identificar la pendiente.
- Olvidar que una mediana pasa por el punto medio del lado opuesto.
- Aplicar mal la fórmula de distancia de un punto a una recta.
Este tipo de reactivos castiga los descuidos. Son ejercicios donde un signo mal puesto o un paso omitido te puede llevar directo a una opción incorrecta, aunque la idea la tengas clara.
Resuelve cada ejercicio con calma, escribe los pasos y revisa bien tus operaciones antes de elegir respuesta. Así es como se entrenan estos temas para el examen real.
Vamos a darle y a seguir subiendo el nivel.
Reactivo 1: Distancia entre dos puntos
Calcula la distancia del punto A (6, 1) al punto B (1, 1).
Reactivo 2: Distancia entre dos puntos
¿Cuál es la distancia entre los puntos P (2, 5) y Q (4, -1)?
Reactivo 3: Punto medio de un segmento
Encuentra las coordenadas del punto medio entre los puntos P (0, 2) y Q (4, 6).
Reactivo 4: Punto medio parametrizado
El punto medio del segmento que une a los puntos A (2m, m + 1) y B (2m, m - 1) es:
Reactivo 5: Pendiente de una recta
La pendiente de la recta 3x + 6y - 1 = 0 es:
Reactivo 6: Cálculo de la pendiente
Calcula la pendiente de la recta cuya función es 2y - 4x + 3 = 0.
Reactivo 7: Ecuación ordinaria de la mediana
La ecuación ordinaria de la mediana del siguiente triángulo, trazada desde el vértice A es:
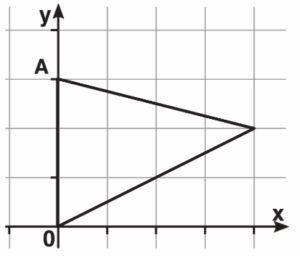
Reactivo 8: Ecuación de la mediana en un triángulo
Un triángulo está conformado por los vértices P (-7, 1), Q (9, 3) y R (3, 5). ¿Cuál es la ecuación de la mediana que pasa por el vértice P?
Reactivo 9: Distancia de un punto a una recta
La distancia del punto (-1, 1) a la recta dada por la ecuación -3x + 4y - 8 = 0 es:
Reactivo 10: Distancia perpendicular
En un marco de referencia representado por un plano cartesiano XY, se localiza un gasoducto sobre la recta 3x + 4y = 2 y una fábrica en el punto (6, 6). Si las distancias se miden en metros, ¿qué longitud de tubo se requiere para conectar perpendicularmente a la fábrica con el gasoducto?


