¿Vas a presentar el examen de admisión a la UNAM, al IPN o el EXANI II? Conoce los temas que siempre vienen en matemáticas. Estamos en la cuarta parte; abajo encontrarás la clase, pero intenta resolverlos primero por tu cuenta, ¿va?

No importa la carrera que vayas a elegir. Estos temas de Matemáticas siempre vienen en los exámenes de admisión, ya sea UNAM, IPN o EXANI II, y dominarlos puede marcar una gran diferencia en tu resultado.
¿Qué vas a aprender?
En esta parte nos vamos a meter de lleno con uno de los bloques que más se repiten: trigonometría y triángulos rectángulos.
Aquí no basta con memorizar fórmulas; tienes que saber leer la figura, identificar datos y elegir correctamente la razón trigonométrica.
Temas del simulador:
- Razones trigonométricas: seno, coseno, tangente, secante y cotangente.
- Triángulos rectángulos y relación entre catetos e hipotenusa.
- Identidades trigonométricas y razones recíprocas.
- Relación entre seno y coseno a partir de un solo dato.
- Aplicaciones de la trigonometría en problemas reales como sombras, alturas y ángulos de elevación.
Este tipo de reactivos suele verse sencillo, pero es donde muchos aspirantes fallan por confundir razones, usar mal la hipotenusa o plantear mal el triángulo. La idea aquí es que aprendas a reconocer rápido qué hacer en cada caso.
Recomendación: intenta resolver cada reactivo antes de ver la solución, como si estuvieras en el examen real.
Vamos con la cuarta parte. Sigamos avanzando y vamos a darle con todo.
Reactivo 1: Razones trigonométricas
Para la figura mostrada, ¿Qué razón se conoce como \sin \theta ?
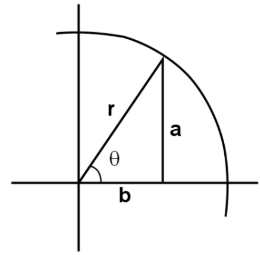
Reactivo 2: Razones trigonométricas
¿Cuánto vale la tangente del ángulo B en el siguiente triángulo?
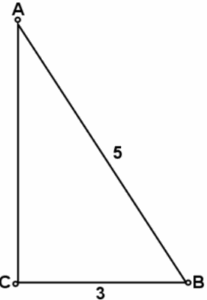
Reactivo 3: Triángulos rectángulos
Sabiendo que el lado opuesto al ángulo B mide 3 y que la tangente del ángulo B vale 3, ¿cuánto vale la hipotenusa del triángulo?
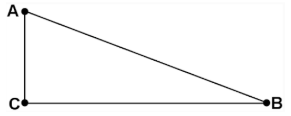
Reactivo 4: Identidades trigonométricas
Si \tan \alpha = \frac{3}{2} y \alpha es un ángulo agudo. ¿Qué valor tiene \cos \alpha ?
Reactivo 5: Identidades trigonométricas
Si \sec \alpha = 5/4 , calcule \tan \alpha .
Reactivo 6: Relación entre seno y coseno
Si se sabe que: \sin(\alpha) = \frac{8}{8.544} , ¿cuál es el valor correspondiente de \cos(\alpha) ?
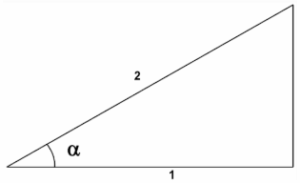
Reactivo 7: Razones trigonométricas y triángulos rectángulos
¿Cuáles son las razones trigonométricas \sin \beta , \cos \beta y \cot \beta que corresponden al siguiente triángulo?
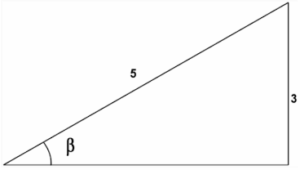
Reactivo 8: Razones trigonométricas y triángulos rectángulos
¿Cuáles son las razones trigonométricas \sin \alpha , \cos \alpha y \tan \alpha que corresponden al siguiente triángulo?
Reactivo 9: Aplicación de las razones trigonométricas
Una persona observa la sombra de un poste mientras el sol proyecta su luz formando un ángulo de 35^\circ con el suelo. Si la sombra mide 7 metros, ¿cuál es la altura del poste?
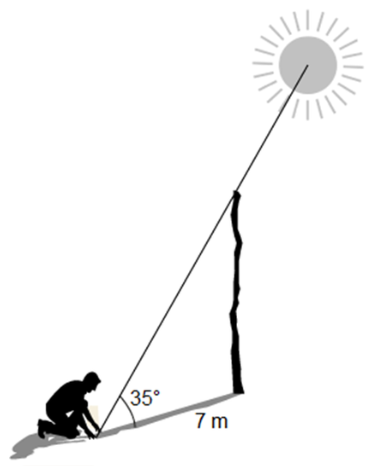
Usa los siguientes valores trigonométricos:
\tan 35^\circ = 0.70 \quad \sin 35^\circ = 0.57 \quad \cos 35^\circ = 0.82
Reactivo 10: Aplicación de las razones trigonométricas
Un guardabosques observa la punta de un árbol a una distancia de 10.0 m. Al hacer esto se forma un ángulo de elevación de 65^\circ respecto a su línea de visión (línea punteada).
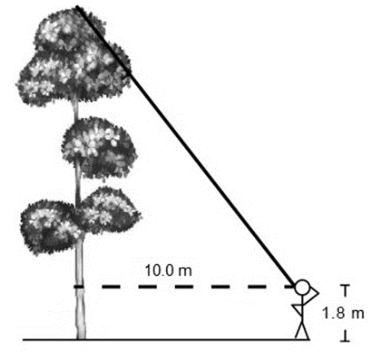
Considere que: \sin 65^\circ = 0.90, \cos 65^\circ = 0.42, \tan 65^\circ = 2.10 .
¿Cuál es la altura del árbol?


